
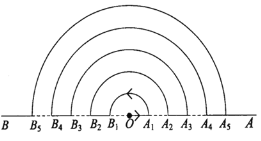
【题目】点O在直线AB上,点A1,A2,A3,……在射线OA上,点B1, B2,B3,……在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,以每秒1个单位长度
的速度按如图所示的箭头方向沿着实线段和以点O为圆心的半圆匀速运动,即从O![]() A1
A1![]() B1
B1![]() B2
B2![]() A2……按此规律,则动点M到达A10点处所需时间为 __________秒.(结果保留π)
A2……按此规律,则动点M到达A10点处所需时间为 __________秒.(结果保留π)
【答案】10+55π .
【解析】
观察动点M从O点出发到A4点,得到点M在直线AB上运动了4个单位长度,在以O为圆心的半圆运动了(π1+π2+π3+π4)单位长度,然后可得到动点M到达A10点处运动的单位长度=4×2.5+(π1+π2+…+π10),然后除以速度即可得到动点M到达A10点处所需时间.
动点M从O点出发到A4点,在直线AB上运动了4个单位长度,在以O为圆心的半圆运动了(π1+π2+π3+π4)单位长度,
∵10=4×2.5,
∴动点M到达A10点处运动的单位长度=4×2.5+(π1+π2+…+π10)=10+55π;
∴动点M到达A10点处运动所需时间=(10+55π)÷1=(10+55π)秒,
故答案为:10+55π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列问题中的关系式,并指出其中的变量和常量.
(1)直角三角形中一个锐角a与另一个锐角β之间的关系;
(2)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展科技创新活动,在一次用电脑程序控制小型赛车进行50m比赛的活动中,“梦想号”和“创新号”两辆赛车在比赛前进行结对练习,两辆车从起点同时出发,“梦想号”到达终点时,“创新号”离终点还差2m.已知“梦想号”的平均速度比“创新号”的平均速度快0.1m/s.
(1)求“创新号”的平均速度;
(2)如果两车重新开始练习,“梦想号”从起点向后退2m,两车同时出发,两车能否同时到达终点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)直接写出AB与AP所满足的数量关系:_____,AB与AP的位置关系:_____;
(2)将△ABC沿直线l向右平移到图2的位置时,EP交AC于点Q,连接AP,BQ,求证:AP=BQ;
(3)将△ABC沿直线l向右平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,试探究AP=BQ是否仍成立?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点E在AC的延长线上,有下列条件∠1=∠2,②∠3=∠4,③∠A=∠DCE,④∠D=∠DCE,⑤∠A+∠ABD=180°,⑥∠A+∠ACD=180°,其中能判断AB∥CD的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学体育组因教学需要本学期购进篮球和排球共100个,共花费2600元,已知篮球的单价是20元![]() 个,排球的单价是30元
个,排球的单价是30元![]() 个.
个.
![]() 篮球和排球各购进了多少个
篮球和排球各购进了多少个![]() 列方程组解答
列方程组解答![]() ?
?
![]() 因该中学秋季开学成立小学部,教学资源实现共享,体育组提出还需购进同样的篮球和排球共30个,但学校要求花费不能超过800元,那么排球最多能购进多少个
因该中学秋季开学成立小学部,教学资源实现共享,体育组提出还需购进同样的篮球和排球共30个,但学校要求花费不能超过800元,那么排球最多能购进多少个![]() 列不等式解答
列不等式解答![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OE平分
,OE平分![]() ,点A、B、C分别是射线OM、OE、ON上的动点
,点A、B、C分别是射线OM、OE、ON上的动点![]() 、B、C不与点O重合
、B、C不与点O重合![]() ,连接AC交射线OE于点
,连接AC交射线OE于点![]() 设
设![]() .
.

![]() 如图1,若
如图1,若![]() ,则
,则
![]() 的度数是______;
的度数是______;
![]() 当
当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______.
______.
![]() 如图2,若
如图2,若![]() ,则是否存在这样的x的值,使得
,则是否存在这样的x的值,使得![]() 中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com