
分析 (1)设1个大餐厅可供x名学生就餐,1个小餐厅可供y名学生就餐,根据“同时开放3个大餐厅和2个小餐厅,可供3160名学生就餐;同时开放2个大餐厅和3个小餐厅,可供2640名学生就餐”,可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据(1)的结论求出同时开放7个大餐厅和3个小餐厅可供就餐的人数,再与6500比较后即可得出结论.
解答 解:(1)设1个大餐厅可供x名学生就餐,1个小餐厅可供y名学生就餐,
根据题意得:$\left\{\begin{array}{l}{3x+2y=3160}\\{2x+3y=2640}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=840}\\{y=320}\end{array}\right.$.
答:1个大餐厅可供840名学生就餐,1个小餐厅可供320名学生就餐.
(2)840×7+320×3=6840(名),
∵6840>6500,
∴如果同时开放10个餐厅,能够供全校的6500名学生就餐,
点评 本题考查了二元一次方程组的应用,解题的关键是:(1)找准等量关系,列出二元一次方程组;(2)根据数量关系求出同时开放10个餐厅可供就餐的人数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全等三角形的对应高、对应中线、对应角平分线相等 | |
| B. | 有两个角和其中一个角的平分线对应相等的两个三角形全等 | |
| C. | 有两条边和其中一边上的中线对应相等的两个三角形全等 | |
| D. | 有两条边和其中一边上的高对应相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
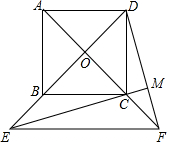 如图,正方形ABCD的对角线AC、BD相交于点O,点E在DB的延长线上,连接EC.过点D作DM⊥EC,垂足为M,DM与AC相交于点F,连接EF.求证:
如图,正方形ABCD的对角线AC、BD相交于点O,点E在DB的延长线上,连接EC.过点D作DM⊥EC,垂足为M,DM与AC相交于点F,连接EF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.
如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com