
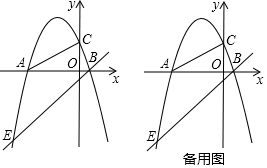
分析 (1)依据锐角三角函数的定义可求得OC=2,从而得到点C(0,2),设抛物线的解析式为y=a(x+4)(x-1),将点C的坐标代入可求得a的值,从而可得到抛物线的解析式,然后依据点Q的坐标是否符合抛物线的解析式可知点Q是否在抛物线上;
(2)先求得直线AC的解析式,设点M的坐标为(m,$\frac{1}{2}$m+2),则点N(m,-$\frac{1}{2}$m2-$\frac{3}{2}$m+2),然后列出MN的长度与m的函数的关系式,利用配方法可求得MN的最大值以及此时m的值,然后依据d和r的关系可判定出以MN为直径的圆与y轴的位置关系;
(3)过点E作ED⊥x轴,垂足为D,过点Q作QF⊥x轴,垂足为F.先求得点E的坐标,然后可证明△DBE和△AQF均为等腰直角三角形,故此在△BAE和△AQP中,∠QAP=∠ABE,然后依据两点间的距离公式求得EB、AQ,AB的长,然后分为△QAP′∽△ABE、△AQP∽△BEA两种情况求解即可.
解答 解:(1)在Rt△AOC中,∠COA=90°,AO=4,tan∠CAB=$\frac{1}{2}$,
∴OC=2.
∴C(0,2).
设抛物线的解析式为y=a(x+4)(x-1),将点C的坐标代入得:-4a=2,解得a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$×(x2+3x-4),即y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2.
当x=1时,y=-$\frac{1}{2}$×(-1)2-$\frac{3}{2}$×(-1)+2=3.
∴点Q(-1,3)在抛物线上.
(2)如图1所示: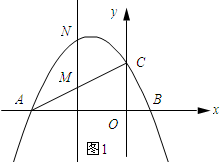
设直线AC的解析式为y=kx+b,将点A、C的坐标代入得:$\left\{\begin{array}{l}{-4k+b=0}\\{b=2}\end{array}\right.$,
解得:k=$\frac{1}{2}$,b=2.
∴直线AC的解析式为y=$\frac{1}{2}$x+2.
设点M的坐标为(m,$\frac{1}{2}$m+2),则点N(m,-$\frac{1}{2}$m2-$\frac{3}{2}$m+2).
∴MN=-$\frac{1}{2}$m2-$\frac{3}{2}$m+2-($\frac{1}{2}$m+2)=-$\frac{1}{2}$(m+2)2+2.
∴当m=-2时,MN的最大值为2.
∴以MN为直径的圆的半径为1.
又∵以MN为直径的圆的圆心到y轴的距离为2,
∴以MN为直径的圆与y轴相离.
(3)如图3所示:过点E作ED⊥x轴,垂足为D,过点Q作QF⊥x轴,垂足为F.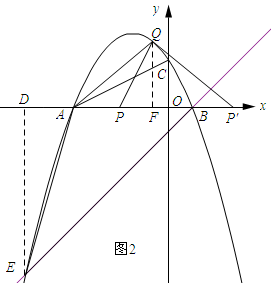
将y=x-1与y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2联立,解得:x=-6,y=-7或x=1,y=0,
∴点E的坐标为(-6,-7).
∴BD=ED=7.
又∵∠EDB=90°
∴∠EBD=45°.
同理∠QAF=45°.
∴∠EBD=∠QAF=45°.
∴∠QAD=135°,90°<∠EAB<135°.
∴点P只能在点A的右侧.
依据两点间的距离公式可知:EB=7$\sqrt{2}$,AQ=3$\sqrt{2}$,AB=5.
当△QAP′∽△ABE时,则$\frac{AP′}{BE}=\frac{AQ}{AB}$,即$\frac{AP′}{7\sqrt{2}}$=$\frac{3\sqrt{2}}{5}$,解得AP′=$\frac{42}{5}$,
∴OP′=$\frac{42}{5}$-4=$\frac{22}{5}$.
当,△AQP∽△BEA时,则$\frac{AP}{AB}=\frac{AQ}{BE}$,即$\frac{AP}{5}=\frac{3\sqrt{2}}{7\sqrt{2}}$,解得:AP=$\frac{15}{7}$,
∴OP=5-$\frac{15}{7}$=$\frac{13}{7}$.
∴点P的坐标为:($\frac{22}{5}$,0)或(-$\frac{13}{7}$,0),
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式,利用二次函数求最大值,直线和圆的位置关系,相似三角形的性质,列出MN的长度与点M的横坐标之间的函数关系是解答问题(2)的关键,分类讨论是解答问题(3)的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
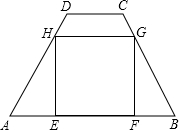 如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.
如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
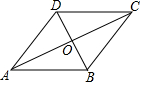 如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )
如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )| A. | AB=BC | B. | AO=BO | C. | ∠DOC=90° | D. | ∠CDO=∠ADO |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示:
王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
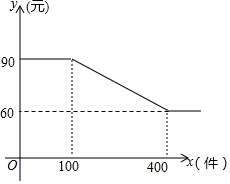 某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.
某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com