
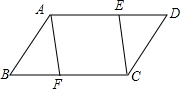
 已知:如图,E、F分别是平行四边形ABCD边AD、BC上的点,并且AF∥CE,
已知:如图,E、F分别是平行四边形ABCD边AD、BC上的点,并且AF∥CE, 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
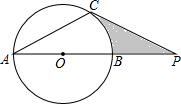 如图,⊙O直径AB与弦AC的夹角∠A=30°,过C点的切线与AB的延长线交于点P.
如图,⊙O直径AB与弦AC的夹角∠A=30°,过C点的切线与AB的延长线交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
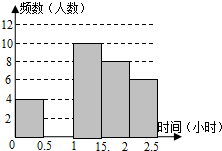 我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.| 时间(小时) | 频数(人数) | 频率 |
| 0≤t<0.5 | 4 | 0.1 |
| 0.5≤t<1 | a | 0.3 |
| 1≤t<1.5 | 10 | 0.25 |
| 1.5≤t<2 | 8 | b |
| 2≤t<2.5 | 6 | 0.15 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )
如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )| A. | 甲比乙的成绩稳定 | B. | 乙比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定谁的成绩更稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
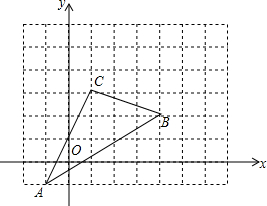 如图,三角形ABC在直角坐标系中,
如图,三角形ABC在直角坐标系中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形纸片ABCD,AB=$\sqrt{3}$,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.
如图,矩形纸片ABCD,AB=$\sqrt{3}$,对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com