
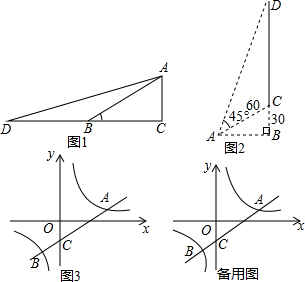
���� ��1����ͼ1��ֻ����˼·һ��˼·���ķ������Ϳɽ�����⣻
��2����ͼ2����Rt��ABC�У����ù��ɶ������AB���������Ǻ�����á�BAC=30�㣮�Ӷ��õ���DAB=75�㣮��Rt��ABD�У��������Ǻ����Ϳ����DB���Ӷ����DC����
��3������ֱ��AB�Ƶ�C��ʱ����ת45�����˫�����ཻ�ڵ�P����ͼ3������C��CD��x�ᣬ����P��PE��CD��E������A��AF��CD��F�����������A��B��C�����꣬�Ӷ����tan��ACF��ֵ���������úͣ�������й�ʽ���tan��PCE=tan��45��+��ACF����ֵ�����P������Ϊ��a��b�������ݵ�P�ڷ�����������ͼ���ϼ�tan��PCE��ֵ���ɵõ�����a��b���������̣������������Ϳɵõ���P�����ꣻ����ֱ��AB�Ƶ�C˳ʱ����ת45�����x���ཻ�ڵ�G����ͼ4���ɢٿ�֪��ACP=45�㣬P����$\frac{4}{3}$��3��������CP��CG������P��PH��y����H����֤��GOC�ס�CHP���������������ε����ʿ����GO���Ӷ��õ���G�����꣬Ȼ���ô���ϵ�������ֱ��CG�Ľ���ʽ��Ȼ��ֱ��CG�뷴���������Ľ���ʽ��ɷ����飬��ȥy���õ�����x�ķ��̣����ø����б�ʽ�ж����õ�������ʵ��������ʱ��P�����ڣ�
��� �⣺��1������һ����ͼ1��
��Rt��ABC�У���C=90�㣬��ABC=30�㣬�ӳ�CB����D��ʹBD=BA������AD��
��AC=1����BD=BA=2��BC=$\sqrt{3}$��
tan��DAC=tan75��=$\frac{DC}{AC}$=$\frac{DB+BC}{AC}$=$\frac{2+\sqrt{3}}{1}$=2+$\sqrt{3}$��
��������tan75��=tan��45��+30�㣩
=$\frac{tan45��+tan30��}{1-tan45��•tan30��}$=$\frac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}$=$\frac{3+\sqrt{3}}{3-\sqrt{3}}$=2+$\sqrt{3}$��
��2�� ��ͼ2��
��ͼ2��
��Rt��ABC��
AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{6{0}^{2}-3{0}^{2}}$=30$\sqrt{3}$��
sin��BAC=$\frac{BC}{AC}$=$\frac{30}{60}$=$\frac{1}{2}$������BAC=30�㣮
�ߡ�DAC=45�㣬���DAB=45��+30��=75�㣮
��Rt��ABD��tan��DAB=$\frac{DB}{AB}$��
��DB=AB•tan��DAB=30$\sqrt{3}$•��2+$\sqrt{3}$��=60$\sqrt{3}$+90��
��DC=DB-BC=60$\sqrt{3}$+90-30=60$\sqrt{3}$+60��
������������CD�ĸ߶�Ϊ��60$\sqrt{3}$+60���ף�
��3������ֱ��AB�Ƶ�C��ʱ����ת45�����˫�����ཻ�ڵ�P����ͼ3��
����C��CD��x�ᣬ����P��PE��CD��E������A��AF��CD��F��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{2}x-1}\\{y=\frac{4}{x}}\end{array}\right.$����
$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2}\\{y=-2}\end{array}\right.$��
���A��4��1������B��-2��-2����
����y=$\frac{1}{2}$x-1����x=0ʱ��y=-1����C��0��-1����OC=1��
��CF=4��AF=1-��-1��=2��
��tan��ACF=$\frac{AF}{CF}$=$\frac{2}{4}$=$\frac{1}{2}$��
��tan��PCE=tan����ACP+��ACF��=tan��45��+��ACF��
=$\frac{tan45��+tan��ACF}{1-tan45��•tan��ACF}$
=$\frac{1+\frac{1}{2}}{1-\frac{1}{2}}$=3����$\frac{PE}{CE}$=3��
���P��������a��b����
����$\left\{\begin{array}{l}{ab=4}\\{\frac{b+1}{a}=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-1}\\{b=-4}\end{array}\right.$��$\left\{\begin{array}{l}{a=\frac{4}{3}}\\{b=3}\end{array}\right.$��
���P��������-1��-4����$\frac{4}{3}$��3����
����ֱ��AB�Ƶ�C˳ʱ����ת45�����x���ཻ�ڵ�G����ͼ4��
�ɢٿ�֪��ACP=45�㣬P����$\frac{4}{3}$��3������CP��CG��
����P��PH��y����H��
���GOC=��CHP=90�㣬��GCO=90��-��HCP=��CPH��
���GOC�ס�CHP��
��$\frac{GO}{CH}$=$\frac{OC}{HP}$��
��CH=3-��-1��=4��PH=$\frac{4}{3}$��OC=1��
��$\frac{GO}{4}$=$\frac{1}{\frac{4}{3}}$=$\frac{3}{4}$��
��GO=3��G��-3��0����
��ֱ��CG�Ľ���ʽΪy=kx+b��
����$\left\{\begin{array}{l}{-3k+b=0}\\{b=-1}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=-1}\end{array}\right.$��
��ֱ��CG�Ľ���ʽΪy=-$\frac{1}{3}$x-1��
����$\left\{\begin{array}{l}{y=-\frac{1}{3}x-1}\\{y=\frac{4}{x}}\end{array}\right.$��
��ȥy����
$\frac{4}{x}$=-$\frac{1}{3}$x-1��
�����ã�x2+3x+12=0��
�ߡ�=32-4��1��12=-39��0��
���û��ʵ������
���P�����ڣ�
����������ֱ��AB�Ƶ�C��ת45�������˫�����ཻ������P������Ϊ��-1��-4����$\frac{4}{3}$��3����
���� ������Ҫ������������Ǻ����Ķ��塢����ǵ����Ǻ���ֵ���ͣ�������й�ʽ���ô���ϵ������һ�κ����Ľ���ʽ������������һ�κ�����ͼ��Ľ��㡢���������ε��ж������ʡ����ɶ����������б�ʽ����һԪ���η��̵�֪ʶ���������������о�����������������ڽ������Ĺ����У��õ��˷������۵���ѧ˼�룬�õ������̽������ѧ��������һ�������¿γ��������̽��������������ϣ��ĺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
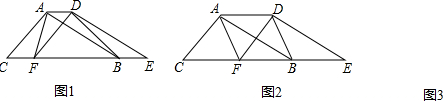
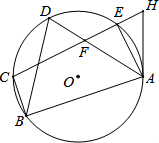 ��ͼ����A��B��C��D��E�ڡ�O�ϣ�AB��CB�ڵ�B��tanD=3��BC=2��HΪCE�ӳ�����һ�㣬��AH=$\sqrt{10}$��CH=5$\sqrt{2}$��
��ͼ����A��B��C��D��E�ڡ�O�ϣ�AB��CB�ڵ�B��tanD=3��BC=2��HΪCE�ӳ�����һ�㣬��AH=$\sqrt{10}$��CH=5$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���Ƽ�ͼ�� ���ε��� ���� | �������� | �������� | ������� | �������� |
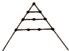 | 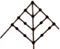 | 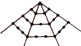 | 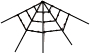 | |
| ��һ�㼸�ε��� | 1 | 1 | 1 | 1 |
| �ڶ��㼸�ε��� | 2 | 3 | 4 | 5 |
| �����㼸�ε��� | 3 | 5 | 7 | 9 |
| �� | �� | �� | �� | �� |
| �����㼸�ε��� | 6 | 11 | 16 | 21 |
| �� | �� | �� | �� | �� |
| ��n�㼸�ε��� | n | 2n-1 | 3n-2 | 4n-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4.0570��109 | B�� | 0.40570��1010 | C�� | 40.570��1011 | D�� | 4.0570��1012 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com