
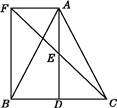
【题目】如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
【答案】(1)证明见解析;(2)当AB=AC时,四边形AFBD是矩形,证明见解析.
【解析】试题分析:(1)根据平行线的性质得到∠AFE=∠DCE,由中点的定义得到AE=DE,根据三角形全等的判定易证得△AFE≌△DCE,利用全等三角形的性质得AF=DC,而AF=BD,即可得到D是BC的中点;
(2)在(1)的基础上,根据全等三角形的性质和有三个角都是直角的四边形是矩形.
试题解析:证明:∵AF∥BC,∴∠AFE=∠ECD.
又∵E为AD的中点,∴AE=DE.
在△AFE与△DCE中,∵ 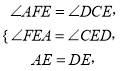
∴△AFE≌△DCE(AAS),∴AF=CD.
又∵AF=BD,∴BD=CD.
(2)解:当AB=AC时,四边形AFBD是矩形.
证法一:由(1)知,D为BC的中点,又∵AB=AC,
∴AD⊥BC.
∵AF∥BC,∴∠DAF=∠ADB=90°.
∵△AFE≌△DCE(已证),∴CE=EF.
∴DE为△BCF的中位线,∴DE∥BF.
∴∠FBD=∠EDC=90°,
∴四边形AFBD是矩形.
证法二:∵AF=BD,AF∥BD,
∴四边形AFBD是平行四边形.
由(1)知,D为BC的中点,又∵AB=AC,
∴AD⊥BC(三线合一),即∠BDA=90°.
∴AFBD是矩形.


科目:初中数学 来源: 题型:
【题目】如图所示,小明家小区空地上有两棵笔直的树![]() 、
、![]() .一天,他在
.一天,他在![]() 处测得树顶
处测得树顶![]() 的仰角
的仰角![]() ,在
,在![]() 处测得树顶
处测得树顶![]() 的仰角
的仰角![]() ,线段
,线段![]() 恰好经过树顶
恰好经过树顶![]() .已知.
.已知. ![]() 、
、![]() 两处的距离为
两处的距离为![]() 米,两棵树之间的距离
米,两棵树之间的距离![]() 米,
米, ![]() 、
、![]() 、
、![]() 、
、![]() 四点在一条直线上,求树
四点在一条直线上,求树![]() 的高度.(
的高度.(![]() ,
, ![]() ,结果精确到
,结果精确到![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
A. a=![]() ,b=
,b=![]() ,c=
,c=![]() B. a=1.5,b=2,c=3
B. a=1.5,b=2,c=3
C. a=6,b=8,c=10 D. a=3,b=4,c=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元,每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() 的解满足x<0,y>0.
的解满足x<0,y>0.
(1)x=________, y=________(用含a的代数式表示);
(2)求a的取值范围;
(3)若2x8y=2m,用含有a的代数式表示m,并求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家-“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.

以![]() 为例,花拉子米的几何解法如下:
为例,花拉子米的几何解法如下:
如图,在边长为![]() 的正方形的两个相邻边上作边长分别为
的正方形的两个相邻边上作边长分别为![]() 和5的矩形,再补上一个边长为5的小正方形,最终把图形补成一个大正方形.
和5的矩形,再补上一个边长为5的小正方形,最终把图形补成一个大正方形.
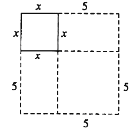
通过不同的方式来表达大正方形的面积,可以将原方程化为![]() )2=39+ ,从而得到此方程的正根是 .
)2=39+ ,从而得到此方程的正根是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①相等的角是对顶角;②在同一平面内,若a∥b,b∥c,则a∥c;③同旁内角互补;④互为邻补角的两角的角平分线互相垂直.⑤平面内,过一点能且只能作一条直线与已知直线垂直.其中真命题有______(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院观众席的座位设置为扇形,且按下列方式排布:

(1)按照上表所表示的变化规律,当排数![]() 每增加1时,座位数
每增加1时,座位数![]() 如何变化?
如何变化?
(2)写出座位数![]() 与排数
与排数![]() 之间的关系式.
之间的关系式.
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com