
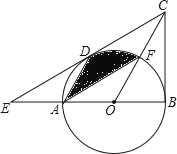
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.
(2)首先证明S阴=S扇形ODF,然后利用扇形面积公式计算即可.
试题解析:(1)证明:连接OD,与AF相交于点G,∵CE与⊙O相切于点D,∴OD⊥CE,∴∠CDO=90°,∵AD∥OC,∴∠ADO=∠1,∠DAO=∠2,∵OA=OD,∴∠ADO=∠DAO,∴∠1=∠2,在△CDO和△CBO中,∵CO=CO,∠1=∠2,OD=OC,∴△CDO≌△CBO,∴∠CBO=∠CDO=90°,∴CB是⊙O的切线.
(2)由(1)可知∠3=∠BCO,∠1=∠2,∵∠ECB=60°,∴∠3=![]() ∠ECB=30°,∴∠1=∠2=60°,∴∠4=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠1=∠ADO,在△ADG和△FOG中,∵∠1=∠ADG,∠FGO=∠AGD,AD=OF,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF=
∠ECB=30°,∴∠1=∠2=60°,∴∠4=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠1=∠ADO,在△ADG和△FOG中,∵∠1=∠ADG,∠FGO=∠AGD,AD=OF,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF=![]() =
= ![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.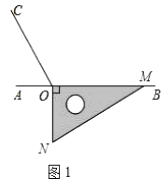
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.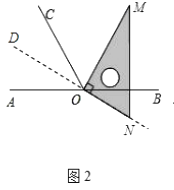
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.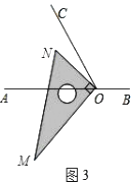
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是 .
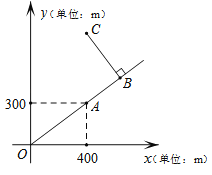
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生某月有零花钱a元,其支出情况如图所示,那么下列说法不正确的是( ) 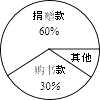
A.该学生捐赠款为0.6a元
B.捐赠款所对应的圆心角为240°
C.捐赠款是购书款的2倍
D.其他消费占10%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数y=x+6,下列结论错误的是( )
A.函数值随自变量增大而增大
B.函数图象与x轴正方向成45°角
C.函数图象不经过第四象限
D.函数图象与x轴交点坐标是(0,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组长度的线段能构成三角形的是( )
A. 1.5cm 3.9cm 2.3cm B. 3.5cm 7.1cm 3.6cm
C. 6cm 1cm 6cm D. 4cm 10cm4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D、C两点分别落在D′、C′的位置,并利用量角器量得∠EFB=66°,则∠AED′等于度. 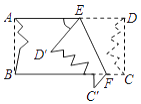
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com