
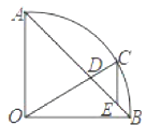
【题目】如图,在扇形![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长是( )
的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
作DF⊥OA于F,证△ADF是等腰直角三角形,∠ODF=30°,得出DF=AF,DF=![]() OF,OD=2OF,求出OF=
OF,OD=2OF,求出OF=![]() ,OD=
,OD=![]() ,CD=OC-OD=4-2
,CD=OC-OD=4-2![]() ,由平行线得出△CDE∽△ODA,进而得出答案.
,由平行线得出△CDE∽△ODA,进而得出答案.
解:作DF⊥OA于F,如图所示:
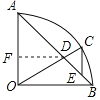
∵OA=OB=2,∠AOB=90°,
∴∠OAB=45°,∠AOD=90°-∠BOC=60°,
∵DF⊥OA,
∴△ADF是等腰直角三角形,∠ODF=30°,
∴DF=AF,DF=![]() OF,OD=2OF,
OF,OD=2OF,
∵AF+OF=OA=2,
∴![]() OF+OF=2,
OF+OF=2,
∴OF=![]() ,
,
∴OD=2![]() -2,
-2,
∴CD=OC-OD=4-2![]() ,
,
∵CE∥OA,
∴△CDE∽△ODA,
∴![]() ,即
,即![]() ,
,
解得:CE=![]() ,
,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,将曲线c1:y=![]() (x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=
(x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=![]() x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6
x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6![]() ,直线y=
,直线y=![]() x交曲线c1于点B,则OB的长( )
x交曲线c1于点B,则OB的长( )
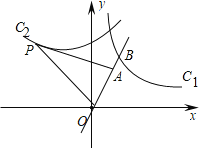
A.2![]() B.5C.3
B.5C.3![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
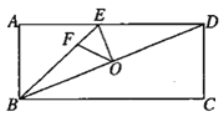
【题目】如图,O为矩形ABCD的对角线BD的中点,点E在AD上,连接EB、EO,BD平分∠EBC,点F在BE上,tan∠OFE=tan∠ABD,若AE=3EF,CD=3,则OD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山上有一座高塔,山脚下有一圆柱形建筑物平台,高塔及山的剖面与圆柱形建筑物平台的剖面ABCD在同一平面上,在点A处测得塔顶H的仰角为35°,在点D处测得塔顶H的仰角为45°,又测得圆柱形建筑物的上底面直径AD为6m,高CD为2.8m,则塔顶端H到地面的高度HG为( )
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)

A.10.8mB.14mC.16.8mD.29.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”,为了改善生态环境,某县政府准备对境内河流进行清淤、疏通河道,同时在人群密集区沿河流修建滨河步道,打造生态湿地公园.
(1)2018年11月至12月,一期工程原计划疏通河道和修建滨河步道里程数共计20千米,其中修建滨河步道里程数是疏通河道里程数的![]() 倍,那么,原计划修建滨河步道多少千米?
倍,那么,原计划修建滨河步道多少千米?
(2)至2018年12月底,一期工程顺利按原计划完成总共耗资840万元,其中疏通河道工程共耗资600万元;2019年二期工程开工后,疏通河道每千米工程费用较一期降低2.5a%,里程数较一期增加3a%;修建滨河步道每千米工程费用较一期上涨2.5a%,里程数较一期增加5a%,经测算,二期工程总费用将比一期增加2a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 城有肥料
城有肥料![]() ,
,![]() 城有肥料
城有肥料![]() .现要把这些肥料全部运往
.现要把这些肥料全部运往![]() 、
、![]() 两乡,
两乡,![]() 乡需要肥料240t,
乡需要肥料240t,![]() 乡需要肥料
乡需要肥料![]() ,其运往
,其运往![]() 、
、![]() 两乡的运费如下表:
两乡的运费如下表:
两城/两乡 | C/(元/ | D/(元/ |
| 20 | 24 |
| 15 | 17 |
设从![]() 城运往
城运往![]() 乡的肥料为
乡的肥料为![]() ,从
,从![]() 城运往两乡的总运费为
城运往两乡的总运费为元,从
![]() 城运往两乡的总运费为
城运往两乡的总运费为![]() 元
元
(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式(不要求写自变量的取值范围);
之间的函数关系式(不要求写自变量的取值范围);
(2)试比较![]() 、
、![]() 两城总运费的大小;
两城总运费的大小;
(3)若![]() 城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是甲、乙两校男、女生人数的统计图.

根据统计图回答问题:
(1)若甲校男生人数为273人,求该校女生人数;
(2)方方同学说:“因为甲校女生人数占全校人数的40%,而乙校女生人数占全校人数的45%,所以甲校的女生人数比乙校女生人数少”,你认为方方同学说的对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
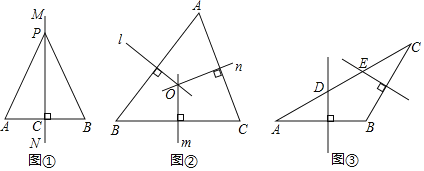
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形,线段的垂直一部分线是线段的对称轴,如图直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 、
、![]() ,将线段
,将线段![]() 与直线
与直线![]() 对称,我们发现
对称,我们发现![]() 与
与![]() 完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
已知:如图,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的任意一点.
上的任意一点.
求证:![]() .
.
图中的两个直角三角形![]() 和
和![]() ,只要证明这两个三角形全等,便可证明
,只要证明这两个三角形全等,便可证明![]() (请写出完整的证明过程)
(请写出完整的证明过程)
请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程,定理应用.
(1)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的垂直平分线.
的垂直平分线.
求证:直线![]() 、
、![]() 、
、![]() 交于点.
交于点.
(2)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_______.
的长为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com