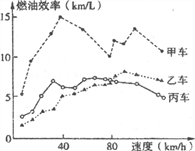
[题目]汽车的“燃油效率是指汽车每消耗1升汽油行驶的里程数. “燃油效率越高表示汽车每消耗1升汽油行驶的里程数越多,“燃油效率越低表示汽车每消耗1升汽油行驶的里程数越少. 下图描述了甲.乙.丙三辆汽车在不同速度下的燃油效率情况. 根据图中提供的信息.下列说法:①以相同速度行驶相同路程.三辆车中.甲车消耗汽油最多②以低于80km/h的速度行驶时. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数. “燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多；“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少. 下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.

根据图中提供的信息，下列说法：

①以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多

②以低于80km/h的速度行驶时，行驶相同路程，三辆车中，乙车消耗汽油最少

③以高于80km/h的速度行驶时，行驶相同路程，乙车比丙车省油

④以80km/h的速度行驶时，行驶100公里，甲车消耗的汽油量约为10升

正确的是________（填写正确结论的序号）.

【答案】③④

【解析】解：①以相同速度行驶相同路程，三辆车中，甲车燃油效率最高，甲车消耗汽油最少，故①错误；

②以低于80km/h的速度行驶时，行驶相同路程，三辆车中，甲车燃油效率最高，甲车消耗汽油最少，故②错误；

C．以高于80km/h的速度行驶时，行驶相同路程，乙车燃油效率大于丙车燃油效率，乙车比丙车省油，故③正确；

D．由图象可知当速度为80km/h时，甲车的燃油效率为10km/L，即甲车行驶10km时，耗油1L，行驶100km时耗油10L，故④正确；

故答案为：③④．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，△ABC在直角坐标系中。

（1）请写出△ABC各点的坐标；

（2）求出△ABC的面积S△ABC；

（3）若把△ABC向上平移2个单位，再向右平移2个单位得△A1B1C1，在图中画出△A1B1C1，并写出△A1B1C1的坐标。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】江南农场收割小麦，已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷，2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷．

（1）每台大型收割机和每台小型收割机1小时收割小麦各多少公顷？

（2）大型收割机每小时费用为300元，小型收割机每小时费用为200元，两种型号的收割机一共有10台，要求2小时完成8公顷小麦的收割任务，且总费用不超过5400元，有几种方案？请指出费用最低的一种方案，并求出相应的费用．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某校在开展 “校园献爱心”活动中，准备向南部山区学校捐赠男、女两种款式的书包．已知男款书包的单价50元/个，女款书包的单价70元/个．

（1）原计划募捐3400元，购买两种款式的书包共60个，那么这两种款式的书包各买多少个？

（2）在捐款活动中，由于学生捐款的积极性高涨，实际共捐款4800元，如果至少购买两种款式的书包共80个，那么女款书包最多能买多少个？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知抛物线经过点A（﹣3，0），F（8，0），B（0，4）三点

（1）求抛物线解析式及对称轴；
（2）若点D在线段FB上运动（不与F，B重合），过点D作DC⊥轴于点C（x，0），将△FCD沿CD向左翻折，点B对应点为点E，△CDE与△FBO重叠部分面积为S．
①试求出S与x之间的函数关系式，并写出自变量取值范围．
②是否存在这样的点C，使得△BDE为直角三角形，若存在，求出C点坐标，若不存在，请说明理由；
（3）抛物线对称轴上有一点M，平面内有一点N，若以A，B，M，N四点组成的四边形为菱形，求点N的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直线AE与CD相交于点B，射线BF平分∠ABC，射线BG在∠ABD内，

（1）若∠DBE的补角是它的余角的3倍，求∠DBE的度数；

（2）在（1）的件下，若∠DBG=∠ABG﹣33°，求∠ABG的度数；

（3）若∠FBG=100°，求∠ABG和∠DBG的度数的差．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知一次函数y=-x+4的图象与x轴、y轴的交点分别为A、B，点P在直线y=2x上.

（1）若点P是一次函数y=-x+4的图象与直线y=2x的交点，求△OBP的面积；

（2）若点P的坐标为(3,6)，求△ABP的面积；

（3）若△ABP的面积为12时，求点P的坐标.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读材料：

一般地，当α、β为任意角时，tan（α+β）与tan（α﹣β）的值可以用下面的公式求得：tan（α±β）=．

例如：tan15°=tan（45°﹣30°）== =

= =．

根据以上材料，解决下列问题：

（1）求tan75°的值；

（2）都匀文峰塔，原名文笔塔，始建于明代万历年间，系五层木塔，文峰塔的木塔年久倾毁，仅存塔基，1983年，人民政府拨款维修文峰塔，成为今天的七层六面实心石塔（图1），小华想用所学知识来测量该铁搭的高度，如图2，已知小华站在离塔底中心A处5.7米的C处，测得塔顶的仰角为75°，小华的眼睛离地面的距离DC为1.72米，请帮助小华求出文峰塔AB的高度．（精确到1米，参考数据≈1.732， ≈1.414）