

 矩形ABCD,∴∠B=90°,即AB⊥BC,
矩形ABCD,∴∠B=90°,即AB⊥BC,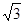 :2
:2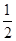 AC,∴∠CAD=30°
AC,∴∠CAD=30°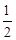 PE=1,∴PH-BE= PA-BE=PR=1。 …………2分
PE=1,∴PH-BE= PA-BE=PR=1。 …………2分

科目:初中数学 来源:不详 题型:解答题
 的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小明同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小明同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示): ;
; ,
, 的中点
的中点 ,
, ,连接
,连接 ;
; 为圆心,
为圆心, 长为半径画弧,交
长为半径画弧,交 的延长线于
的延长线于 ;
; 作
作 ⊥
⊥ ,交
,交 的延长线于
的延长线于 。
。 为黄金矩形。
为黄金矩形。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ABCD中,BC=7厘米,CD=5厘米,∠D=50°,
ABCD中,BC=7厘米,CD=5厘米,∠D=50°,
| A.∠C="130°" | B.∠BED=130° |
| C.AE=5厘米 | D.ED=2厘米 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com