练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

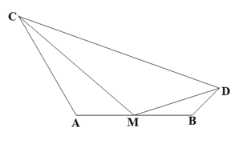
    【题目】如图，AC，BD在AB的同侧，AC＝10，BD＝3，AB＝8，点M为AB的中点，若∠CMD＝120°，则CD的最大值是____．

    【答案】17

    【解析】

    如图，作点A关于CM的对称点A′，点B关于DM的对称点B′，证明△A′MB′为等边三角形，即可解决问题．

    解：如图，作点A关于CM的对称点A′，点B关于DM的对称点B′．

    ∴AM=AM=AB，BM=BM=AB，BD=BD，AC=AC，
    ∵∠CMD＝120°，
    ∴∠AMC＋∠DMB＝60°，
    ∴∠CMA′＋∠DMB′＝60°，
    ∴∠A′MB′＝60°，
    ∵MA′＝MB′，
    ∴△A′MB′为等边三角形
    ∵CD≤CA′＋A′B′＋B′D＝CA＋AM＋BD＝10＋4＋3＝17，
    ∴CD的最大值为：17，
    故答案为：17．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，CD∥AB，∠DCB=70°，∠CBF=20°，∠EFB=130°，

    （1）问直线EF与AB有怎样的位置关系？加以证明；

    （2）若∠CEF=70°，求∠ACB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校为了了解七年学生跳绳情况，从七年级学生中随机抽查了50名学生进行1分钟跳绳测试，并对测试结果统计后绘制了如下不完整统计图表，请根据图表中的信息解答下列问题．

    组别

    次数

    频数（人）

    百分比

    1

    60≤x＜90

    5

    10%

    2

    90≤x＜120

    5

    b

    3

    120≤x＜150

    18

    36%

    4

    150≤x＜180

    a

    c

    5

    180≤x＜210

    2

    4%

    合计

    50

    1

    （1）直接写出a＝　 ，b＝　 ，c＝　 ；

    （2）请补全频数分布直方图；

    （3）若该校七年级共有学生400人，请你估计该校七年级学生跳绳次数在90≤x＜150范围的学生约有多少人？（

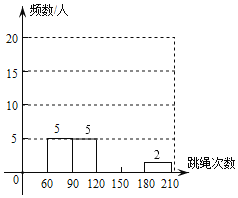
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，OA＝2，OB＝3，现同时将点A，B分别向上平移2个单位，再向右平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD．

    (1)求点C、D的坐标及四边形ABDC的面积；

    (2)若点Q在线的CD上移动(不包括C，D两点)．QO与线段AB，CD所成的角∠1与∠2如图所示，给出下列两个结论：①∠1+∠2的值不变；②的值不变，其中只有一个结论是正确的，请你找出这个结论，并求出这个值．

    (3)在y轴正半轴上是否存在点P，使得S△CDP＝S△PBO？如果有，试求出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，线段AE⊥BD于C，AB＝DE，∠A＝30°，∠E＝50°，F是DE的中点，则∠DBF的度数等于（ ）

    A.10°B.20°C.30°D.40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行超价收费，为更好的决策，自来水公司随机抽取了部分用户的用水量数据，并绘制了如图不完整的统计图，（每组数据包括在右端点但不包括左端点），请你根据统计图解答下列问题：

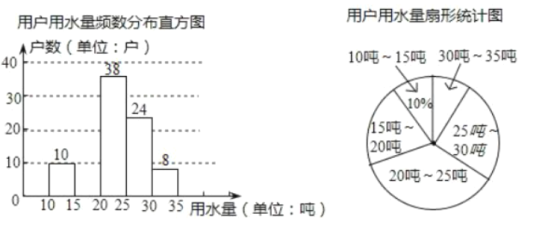
    （1）此次抽样调查的样本容量是 ．

    （2）补全频数分布直方图，求扇形图中“吨—吨”部分的圆心角的度数.

    （3）如果自来水公司将基本用水量定为每户吨，那么该地区万用户中约有多少用户的用水全部享受基本价格？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中∠B=45°，∠C=30°，点D为BC边上任意一点，连接AD，将线段AD绕A顺时针旋转90°，得到线段AE，连接DE．

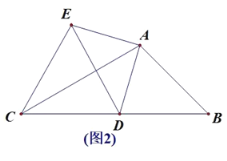
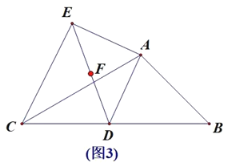
    （1）如图1，点E落在BA的延长线上时，∠EDC= （度）直接填空．

    （2）如图2，点D在运动过程中，DE⊥AC时，AB=4 ，求DE的值．

    （3）如图3，点F为线段DE中点，AB=，求出动点D从B运动到C，点F经过的路径长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AB=12，BC=5，BE⊥DC交DC的延长线于点E.

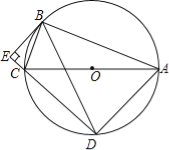
    （1）求证：∠BCA=∠BAD；

    （2）求DE的长；

    （3）求证:BE是⊙O的切线.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，菱形的对角线、相交于点，过点作且，连接、，连接交于点．

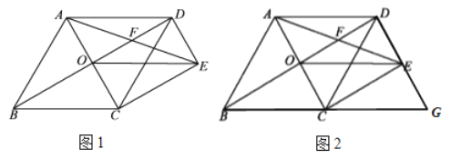
    （1）求证：；

    （2）如图2，延长和相交于点，不添加任何辅助线的情况下，直接写出图中所有的平行四边形．（除四边形和四边形外）

    查看答案和解析>>

    同步练习册答案