
 ШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=3ЃЌAB=5ЃЌЕуPДгЕуCГіЗЂбиCAвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌЕНДяЕуAКѓСЂПЬвддРДЕФЫйЖШбиACЗЕЛиЃЌЕуQДгЕуAГіЗЂбиABвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЎАщЫцзХPЁЂQЕФдЫЖЏЃЌDEБЃГжДЙжБЦНЗжPQЃЌЧвНЛPQгкЕуDЃЌНЛелЯпQB-BC-CPгкЕуEЃЎЕуPЁЂQЭЌЪБГіЗЂЃЌЕБЕуQЕНДяЕуBЪБЭЃжЙдЫЖЏЃЌЕуPвВЫцжЎЭЃжЙЃЎЩшЕуPЁЂQдЫЖЏЕФЪБМфЪЧtУыЃЈtЃО0ЃЉЃЎ
ШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=3ЃЌAB=5ЃЌЕуPДгЕуCГіЗЂбиCAвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌЕНДяЕуAКѓСЂПЬвддРДЕФЫйЖШбиACЗЕЛиЃЌЕуQДгЕуAГіЗЂбиABвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЎАщЫцзХPЁЂQЕФдЫЖЏЃЌDEБЃГжДЙжБЦНЗжPQЃЌЧвНЛPQгкЕуDЃЌНЛелЯпQB-BC-CPгкЕуEЃЎЕуPЁЂQЭЌЪБГіЗЂЃЌЕБЕуQЕНДяЕуBЪБЭЃжЙдЫЖЏЃЌЕуPвВЫцжЎЭЃжЙЃЎЩшЕуPЁЂQдЫЖЏЕФЪБМфЪЧtУыЃЈtЃО0ЃЉЃЎЗжЮі ЃЈ1ЃЉЯШЧѓPCЃЌдйЧѓAPЃЌШЛКѓЧѓAQЃЌдйгЩШ§НЧаЮЯрЫЦЧѓQЕНACЕФОрРыЃЛ
ЃЈ2ЃЉЙ§ЕуQзїQFЁЭACгкЕуFЃЌЯШЧѓBCЃЌдйгУtБэЪОQFЃЌШЛКѓЕУГіSЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЕБDEЁЮQBЪБЃЌЕУЫФБпаЮQBEDЪЧжБНЧЬнаЮЃЌгЩЁїAPQЁзЁїABCЃЌгЩЯпЖЮЕФЖдгІБШР§ЙиЯЕЧѓЕУtЃЌгЩPQЁЮBCЃЌЫФБпаЮQBEDЪЧжБНЧЬнаЮЃЌЁїAQPЁзЁїABCЃЌгЩЯпЖЮЕФЖдгІБШР§ЙиЯЕЧѓtЃЛ
ЃЈ4ЃЉЂйЕквЛжжЧщПіЕуPгЩCЯђAдЫЖЏЃЌDEОЙ§ЕуCЁЂСЌНгQCЃЌзїQGЁЭBCгкЕуGЃЌгЩPC2=QC2НтЕУtЃЛЂкЕкЖўжжЧщПіЃЌЕуPгЩAЯђCдЫЖЏЃЌDEОЙ§ЕуCЃЌгЩЭМСаГіЯрЛЅЙиЯЕЃЌЧѓНтtЃЎ
НтД№ НтЃКЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуQзїQFЁЭACгкЕуFЃЌ
ЁпAC=3ЃЌЕуPДгЕуCГіЗЂбиCAвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌ
ЁрЕБt=2ЪБЃЌAP=3-2=1ЃЛ
дкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=3ЃЌAB=5ЃЎ
ЁрBC=4ЃЌ
ЁпQFЁЭACЃЌBCЁЭACЃЌ
ЁрQFЁЮBCЃЌ
ЁрЁїACBЁзЁїAFQЃЌ
Ёр$\frac{AQ}{AB}$=$\frac{QF}{BC}$ЃЌ
Ёр$\frac{2}{5}$=$\frac{QF}{4}$ЃЌ НтЕУЃКQF=$\frac{8}{5}$ЃЛ
НтЕУЃКQF=$\frac{8}{5}$ЃЛ
ЙЪД№АИЮЊЃК1ЃЌ$\frac{8}{5}$ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуQзїQFЁЭACгкЕуFЃЌ
ШчЭМ1ЃЌAQ=CP=tЃЌ
ЁрAP=3-tЃЎ
гЩЁїAQFЁзЁїABCЃЌ
ЕУQF$\frac{QF}{4}$=$\frac{t}{5}$ЃЎ
ЁрQF=$\frac{4}{5}$tЃЎ
ЁрS=$\frac{1}{2}$ЃЈ3-tЃЉ•$\frac{4}{5}$tЃЌ МДS=-$\frac{2}{5}$t2+$\frac{6}{5}$tЃЛ
МДS=-$\frac{2}{5}$t2+$\frac{6}{5}$tЃЛ
ЃЈ3ЃЉФмЃЎ
ЂйЕБгЩЁїAPQЁзЁїABCЃЌDEЁЮQBЪБЃЌШчЭМ2ЃЎ
ЁпDEЁЭPQЃЌ
ЁрPQЁЭQBЃЌЫФБпаЮQBEDЪЧжБНЧЬнаЮЃЌ
ДЫЪБЁЯAQP=90ЁуЃЎ
гЩЁїAPQЁзЁїABCЃЌЕУ$\frac{AQ}{AC}$=$\frac{AP}{AB}$ЃЌ
МД$\frac{t}{3}$=$\frac{3-t}{5}$ЃЎ НтЕУt=$\frac{9}{8}$ЃЛ
НтЕУt=$\frac{9}{8}$ЃЛ
ЂкШчЭМ3ЃЌЕБPQЁЮBCЪБЃЌDEЁЭBCЃЌЫФБпаЮQBEDЪЧжБНЧЬнаЮЃЎ
ДЫЪБЁЯAPQ=90ЁуЃЎ
гЩЁїAQPЁзЁїABCЃЌЕУ$\frac{AQ}{AB}$=$\frac{AP}{AC}$ЃЌ
МД$\frac{t}{5}$=$\frac{3-t}{3}$ЃЎ
НтЕУt=$\frac{15}{8}$ЃЌ
злЩЯЃКдкЕуEДгBЯђCдЫЖЏЕФЙ§ГЬжаЃЌЕБt=$\frac{9}{8}$Лђ$\frac{15}{8}$ЪБЃЌЫФБпаЮQBEDФмГЩЮЊжБНЧЬнаЮЃЛ
ЃЈ4ЃЉt=$\frac{5}{2}$Лђt=$\frac{45}{14}$ЃЎ ЂйЕуPгЩCЯђAдЫЖЏЃЌDEОЙ§ЕуCЃЎ
ЂйЕуPгЩCЯђAдЫЖЏЃЌDEОЙ§ЕуCЃЎ
СЌНгQCЃЌзїQGЁЭBCгкЕуGЃЌШчЭМ4ЃЎ
ЁпsinB=$\frac{AC}{AB}$=$\frac{3}{5}$=$\frac{QG}{BQ}$ЃЌ
ЁрQG=$\frac{3}{5}$ЃЈ5-tЃЉЃЌ
ЭЌРэBG=$\frac{4}{5}$ЃЈ5-tЃЉЃЌ
ЁрCG=4-$\frac{4}{5}$ЃЈ5-tЃЉЃЌ
ЁрPC=tЃЌQC2=QG2+CG2=[$\frac{3}{5}$ЃЈ5-tЃЉ]2+[4-$\frac{4}{5}$ЃЈ5-tЃЉ]2ЃЎ
ЁпCDЪЧPQЕФжаДЙЯпЃЌ
ЁрPC=QC
дђPC2=QC2ЃЌ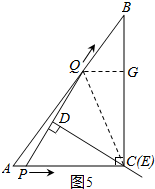 ЕУt2=[$\frac{3}{5}$ЃЈ5-tЃЉ]2+[4-$\frac{4}{5}$ЃЈ5-tЃЉ]2ЃЌ
ЕУt2=[$\frac{3}{5}$ЃЈ5-tЃЉ]2+[4-$\frac{4}{5}$ЃЈ5-tЃЉ]2ЃЌ
НтЕУt=$\frac{5}{2}$ЃЛ
ЃЌЂкЕуPгЩAЯђCдЫЖЏЃЌDEОЙ§ЕуCЃЌШчЭМ5ЃЎ
PC=6-tЃЌПЩжЊгЩPC2=QC2ПЩжЊЃЌ
QC2=QG2+CG2
ЃЈ6-tЃЉ2=[$\frac{3}{5}$ЃЈ5-tЃЉ]2+[4-$\frac{4}{5}$ЃЈ5-tЃЉ]2ЃЌ
МДt=$\frac{45}{14}$ЃЎ
ЕуЦР ДЫЬтЪєгкШ§НЧаЮЕФзлКЯЬтЃЎПМВщСЫЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЁЂжБНЧЬнаЮЕФаджЪЁЂЙДЙЩЖЈРэвдМАШ§НЧКЏЪ§ЕШжЊЪЖЃЌзЂвтзМШЗзїГіИЈжњЯпЃЌеЦЮеЗНГЬЫМЯыгыЗжРрЬжТлЫМЯыЕФгІгУЪЧНтДЫЬтЕФЙиМќЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЫљЪОЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯC=90ЉbЃЌАбЕуAбиBDелелЕўЃЌЧЁКУТфдкBCБпЩЯЕФЕуEДІЃЌСЌНгDEЃЎ
ШчЭМЫљЪОЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯC=90ЉbЃЌАбЕуAбиBDелелЕўЃЌЧЁКУТфдкBCБпЩЯЕФЕуEДІЃЌСЌНгDEЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌе§ЗНаЮPQMNКЭе§ЗНаЮMABCжаЃЌЕуNдкCMЩЯЃЌQM=2ЃЌAM=6ЃЌDЪЧPBЕФжаЕуЃЌФЧУДDMЕФГЄЪЧ2$\sqrt{5}$ЃЎ
ШчЭМЃЌе§ЗНаЮPQMNКЭе§ЗНаЮMABCжаЃЌЕуNдкCMЩЯЃЌQM=2ЃЌAM=6ЃЌDЪЧPBЕФжаЕуЃЌФЧУДDMЕФГЄЪЧ2$\sqrt{5}$ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com