
分析 在BF上截取PN=CN,连接CN,先证明△ABE≌△BCF,得出∠BAE=∠CBF,∠AEB=∠BFC,进而证得∠APF=∠BAE+∠ABF=60°,∠CPF=30°,得出∠CNF=60°,再证明△PBE≌△NCF,得出PB=CN,即可证得BN=2PN,然后通过△APB≌△BNC,PA=BN=2PN,进而通过直角三角函数求得PC=$\frac{\sqrt{3}}{2}$PA,CM=$\frac{\sqrt{3}}{3}$PC,最后根据平行线分线段定理得出$\frac{CM}{PA}$=$\frac{CF}{AF}$,就可求得CF的长,即BE的长.
解答  解:在BF上截取PN=CN,连接CN,
解:在BF上截取PN=CN,连接CN,
在△ABE和△BCF中
$\left\{\begin{array}{l}{AB=AC}\\{∠ABE=∠BCF=60°}\\{BE=CF}\end{array}\right.$
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,∠AEB=∠BFC,
∵∠CBF+∠ABF=60°,
∴∠APF=∠BAE+∠ABF=60°,
∵AE⊥PC,
∴∠CPF=30°,
∵PN=CN,
∴∠PCN=30°,
∴∠CNF=60°,
在△PBE和△NCF中,
$\left\{\begin{array}{l}{∠BPE=∠CNF=60°}\\{∠PEB=∠NFC}\\{BE=CF}\end{array}\right.$,
∴△PBE≌△NCF(AAS),
∴PB=CN,
∴PN=PB,
∴BN=2PN,
∵∠APF=∠BAP+∠PBA=60°,∠CBN+∠ABP=60°,
∴∠BAP=∠CBN,
在△APB和△BNC中,
$\left\{\begin{array}{l}{∠BAP=∠CBN}\\{∠APB=∠BNC=120°}\\{AB=AC}\end{array}\right.$,
∴△APB≌△BNC(AAS),
∴PA=BN=2PN,
作CM∥AE,交BF的延长线于M,作NK⊥PC于K,则PC⊥CM,PK=$\frac{1}{2}$PC,
∵∠CPF=30°,
∴PK=$\frac{\sqrt{3}}{2}$PN,
∴PC=$\frac{\sqrt{3}}{2}$PA,
∴PA=$\frac{2\sqrt{3}}{3}$PC,
在RT△PCM中,∠CPF=30°,
∴CM=$\frac{\sqrt{3}}{3}$PC,
∵CM∥AE,
∴$\frac{CM}{PA}$=$\frac{CF}{AF}$,即$\frac{\frac{\sqrt{3}}{3}PC}{\frac{2\sqrt{3}}{3}PC}$=$\frac{CF}{1-CF}$,
∴CF=$\frac{1}{3}$.
∴BE=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了三角形全等的判定和性质,等边三角形的性质,解直角三角函数,平行线分线段成比例定理等,作出辅助线构建全等三角形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
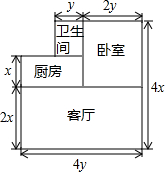 (1)一家住房的结构如图所示,这家房子的主人打算把卧室以外的部分都铺上地砖,至少需要多少m2的地砖?如果每1m2地砖的价格是a元钱,则购买所需地砖至少需要多少元?
(1)一家住房的结构如图所示,这家房子的主人打算把卧室以外的部分都铺上地砖,至少需要多少m2的地砖?如果每1m2地砖的价格是a元钱,则购买所需地砖至少需要多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是一大型广告牌截面,CD是一堵墙的横截面,AB,CD均与地面BE垂直,广告牌的安全拉线ACE要越过围墙(B、D、E三点在同一直线上),已知:AB=5米,CD=3米,∠CED=45°,∠ACE=165°,求拉线ACE的长l(参考数据$\sqrt{2}$≈1.4)
如图,AB是一大型广告牌截面,CD是一堵墙的横截面,AB,CD均与地面BE垂直,广告牌的安全拉线ACE要越过围墙(B、D、E三点在同一直线上),已知:AB=5米,CD=3米,∠CED=45°,∠ACE=165°,求拉线ACE的长l(参考数据$\sqrt{2}$≈1.4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com