练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，将一张长方形的纸片连续对折，对折时每次折痕与上次的折痕保持平行，对折一次得到1条折痕(图中虚线)，对折二次得到3条折痕，对折三次得到7条折痕，那么对折2018次后可以得到________条折痕．

    【答案】(22018－1)

    【解析】

    观察图形，对折1次，是2-1=1条折痕，对折2次22-1=3条折痕，对折3次23-1=7条折痕，对折4次24-1=15条折痕，…，据此可得，对折n次是2n-1条折痕，据此即可解答问题．

    根据题干分析可得：

    对折1次，是2-1=1条折痕，

    对折2次22-1=3条折痕，

    对折3次23-1=7条折痕，

    对折4次24-1=15条折痕，…，

    对折n次是2n-1条折痕，

    当n=2018时，折痕有：22018-1（条）.

    故答案为：22018-1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3＋2＝(1＋)2，善于思考的小明进行了以下探索：

    设a＋b＝(m＋n)2(其中a、b、m、n均为正整数)，则有a＋b＝m2＋2n2＋2mn，

    ∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把a＋b的式子化为平方式的方法．

    请你仿照小明的方法探索并解决下列问题：

    （1）当a、b、m、n均为正整数时，若a＋b＝(m＋n)2，用含m、n的式子分别表示a、b，得：a＝ , b＝ .

    （2）利用所探索的结论，找一组正整数a、b、m、n填空： + = ( + )2；(答案不唯一)

    （3）若a＋4＝(m＋n)2 ,且a、m、n均为正整数,求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度，随机抽取了部分学生进行调查（每人限选1项），现将调查结果绘制成如下两幅不完整的统计图，根据图中所给的信息解答下列问题．

    （1）喜爱动画的学生人数和所占比例分别是多少？

    （2）请将条形统计图补充完整；

    （3）若该校共有学生1000人，依据以上图表估计该校喜欢体育的人数约为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在⊙O中，AB是直径，点D是⊙O上的一点，点C是 的中点，弦CM垂直AB于点F，连接AD，交CF于点P，连接BC，∠DAB=30°．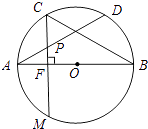

    （1）求∠ABC的度数；
    （2）若CM=4 ，求 的长度．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABO的三个顶点的坐标分别为O(0，0)，A(5，0)，B(2，4)．

    (1)求△OAB的面积；

    (2)若O，A两点的位置不变，P点在什么位置时，△OAP的面积是△OAB面积的2倍？

    (3)若B(2，4)，O(0，0)不变，M点在x轴上，M点在什么位置时，△OBM的面积是△OAB面积的2倍？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请阅读下列材料：

    计算：.

    解法一：原式＝

    解法二：原式＝(－)÷[( )－( )]＝÷＝－×3＝－.

    解法三：原式的倒数为()÷(－)＝×(－30)－×(－30)＋×(－30)－×(－30)＝－20＋3－5＋12＝－10，

    故原式＝－.

    (1)上述解法得出的结果不同，肯定有错误的解法，你认为解法________是错误的，在正确的解法中，你认为解法________最简捷；

    (2)利用(1)中你认为最简捷的解法计算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求两个正整数的最大公约数是常见的数学问题，中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法——更相减损术，术曰：“可半者半之，不可半者，副置分母、子之数，以少成多，更相减损，求其等也，以等数约之．”意思是说，要求两个正整数的最大公约数，先用较大的数减去较小的数，得到差，然后用减数与差中的较大数减去较小数，以此类推，当减数与差相等时，此时的差(或减数)即为这两个正整数的最大公约数．例如：求91与56的最大公约数：

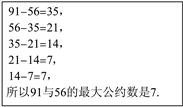
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等腰△AOB，AO=AB=5，OB=6．以O为原点，以OB边所在的直线为x轴，以垂直于OB的直线为y轴建立平面直角坐标系．

    （1）求点A的坐标；

    （2）若点A关于y轴的对称点为M，点N的横、纵坐标之和等于点A的横坐标，请在图中画出一个满足条件的△AMN，并直接在图上标出点M，N的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学生的学业负担过重会严重影响学生对待学习的态度．为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：

    （1）此次抽样调查中，共调查了 名学生；

    （2）将图①补充完整；

    （3）求出图②中C级所占的圆心角的度数；

    （4）根据抽样调查结果，请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标（达标包括A级和B级）？

    查看答案和解析>>

    同步练习册答案