
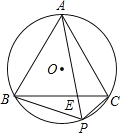
【题目】如图,正![]() 内接于
内接于![]() 是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() 图中共有6对相似三角形.
图中共有6对相似三角形.
其中,正确结论的个数为![]()
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】延长BP到D,使PD=PC,连接CD,可得∠CPD=∠BAC=60°,
则△PCD为等边三角形,
∵△ABC为正三角形,
∴BC=AC,
∵∠PBC=∠CAP,∠CPA=∠CDB,
∴△APC≌△BDC(AAS),
∴PA=DB=PB+PD=PB+PC,故①正确;
由①知△PBE∽△PAC,则![]() ,
, ![]() ,
,
∴![]() ≠1,
≠1,
∴②错误;
∵∠BAC=60°,
∴∠PBC=120°,故③正确;
∵∠CAP=∠EBP,∠BPE=∠CPA,
∴△PBE∽△PAC,
∴![]() ,
,
∴PAPE=PBPC,故④正确;
∵△ABE∽△CPE,△AEC∽△BEP,△ACE∽△APC,△APC∽△BPE,△ABE∽△APB,△CPE∽△APB共6对相似三角形,故⑤正确,
故选B.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
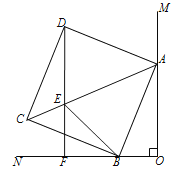
【题目】如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.
(1)求证BE=DE;
(2)判断DF与ON的位置关系,并说明理由;
(3)△BEF的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 13×7 的网格中,每个小正方形边长都是 1,其顶点叫做格点,如图 A、B、D、E 均为格点,![]() ABD 为格点三角形.
ABD 为格点三角形.

(1)请在给定的网格中画 ABCD,要求 C 点在格点上;
(2)在(1)中 ABCD 右侧,以格点 E 为其中的一个顶点,画格点![]() EFG,并使 EF=5,FG=3,EG=
EFG,并使 EF=5,FG=3,EG=![]()
(3)先将(2)中的线段 EF 向右平移 6 个单位、再向下平移 l 个单位到 MP 的位置,再以 MP 为对角线画矩形 MNPQ(M、N、P、Q 按逆时针方向排列),直接写出矩形 MNPQ 的面积为 ______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,一条生产线的流水线上依次有5个机器人,它们站立的位置在数轴上依次用点A1,A2,A3,A4,A5表示.
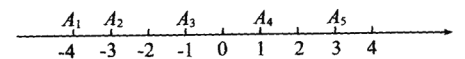
(1)若原点是零件的供应点,5个机器人分别到供应点取货的总路程是多少?
(2)若将零件的供应点改在A1,A3,A5中的其中一处,并使得5个机器人分别到达供应点取货的总路程最短,你认为应该在哪个点上?通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
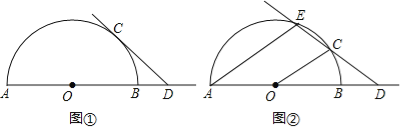
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
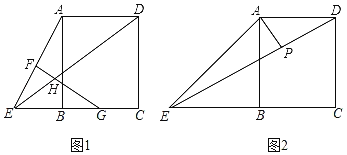
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=![]() 和y=
和y=![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①![]() ;②阴影部分面积是
;②阴影部分面积是![]() (k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )

A.①②B.①④C.③④D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com