
 如图,在△ABC中,∠MAC为∠BAC的外角,P为∠MAC的平分线的反向延长线上一点(A除外).
如图,在△ABC中,∠MAC为∠BAC的外角,P为∠MAC的平分线的反向延长线上一点(A除外).分析 (1)如图作PG⊥CA于G,PN⊥AB于N.由△PAG≌△PAN,得到AG=AN,在Rt△PCG中,PC>CG即PC>AC+AG,在Rt△PBN中,PB>BN即PB>AB-AN,由此根据不等式性质即可证明.
(2)首先证明P、B、C、A四点共圆,推出PB=PC,再证明△PCG≌△PBN,得CG=BN,由此即可解决问题.
解答 解:(1)如图作PG⊥CA于G,PN⊥AB于N.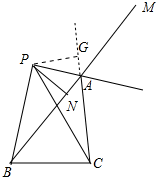
∵PA平分∠BAG,PG⊥AG,PN⊥AN,
∴PG=PN,
在Rt△PAG和Rt△PAN中,
$\left\{\begin{array}{l}{PA=PA}\\{PG=PN}\end{array}\right.$,
∴△PAG≌△PAN,
∴AG=AN,
在Rt△PCG中,PC>CG即PC>AC+AG,
在Rt△PBN中,PB>BN即PB>AB-AN,
∴PB+PC>(AC+AG)+(AB-AN),
∴PB+PC>AB+AC.
(2)如图,作PG⊥CA于G.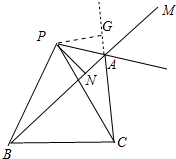
∵∠BPC=∠BAC,
∴P、B、C、A四点共圆,
∴∠PAG=∠PBC,∠PAB=∠ACB,
∵∠PAG=∠PAB,
∴∠PBC=∠PCB,
∴PB=PC,
由(1)可知,PG=PN,AG=AN,
在Rt△PCG和△PBN中,
$\left\{\begin{array}{l}{PB=PC}\\{PN=PG}\end{array}\right.$,
∴△PCG≌△PBN,
∴CG=BN,
∴AB-AC=(BN+AN)-(CG-AG)=AN+AG=2AN.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定、垂线段最短、四点共圆等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,构造全等三角形,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解青年人的体质状况,选择运动员进行调查 | |
| B. | 为了解全市老年人的健康状况,选择公园中散步的老人进行调查 | |
| C. | 为了解某省所有家庭的用电情况,随机抽查某个小区所有家庭的用电情况 | |
| D. | 为了解10箱某种汽水的质量,随机抽取10瓶进行鉴定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一块直角三角形形状的绿地,量得两直角边长分别为6,8.现在要将绿地扩充成等腰三角形,且扩充的图形是以8长的边为直角边的直角三角形,求扩充后等腰三角形绿地的三边长的平方和.
如图是一块直角三角形形状的绿地,量得两直角边长分别为6,8.现在要将绿地扩充成等腰三角形,且扩充的图形是以8长的边为直角边的直角三角形,求扩充后等腰三角形绿地的三边长的平方和.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④⑥ | C. | ③④⑤ | D. | ①⑤⑥ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com