
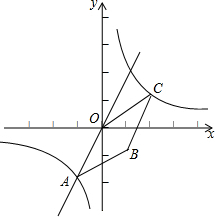
 (2013•十堰)如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).
(2013•十堰)如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,-2).| 5 |
| k |
| x |
| 5 |
| k |
| x |
| k |
| x |
| 2 |
| x |
| 12+22 |
| 5 |
| 5 |
| 2 |
| x |
| 22+12 |
| 5 |


科目:初中数学 来源: 题型:
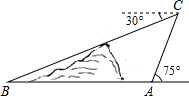 (2013•十堰)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为
(2013•十堰)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
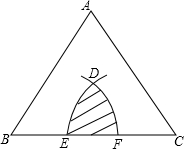 (2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当
(2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当| 2 |
| π |
| 2 |
| 4π |
| 3 |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
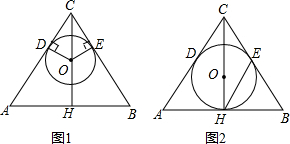 (2013•十堰)如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.
(2013•十堰)如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com