
分析 利用描点法可画出这三个函数的图象,分别由图象可得出开口方向、对称轴及顶点坐标.
解答 解:如图,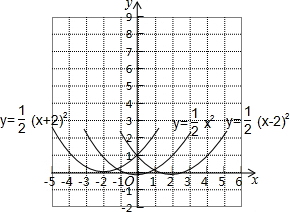
y=$\frac{1}{2}$x2的图象向右平移2个单位得到y=$\frac{1}{2}$(x-2)2的图象,
y=$\frac{1}{2}$x2的图象向左平移2个单位得到y=$\frac{1}{2}$(x+2)2的图象,
y=$\frac{1}{2}$x2的开口向上,对称轴为直线x=0,顶点坐标为(0,0);
y=$\frac{1}{2}$(x-2)2的开口向上,对称轴为直线x=2,顶点坐标为(2,0);
y=$\frac{1}{2}$(x+2)2的开口向上,对称轴为直线x=-2,顶点坐标为(-2,0).
点评 本题主要考查函数图象的画法及二次函数的图象的性质,掌握基本的描点法作函数图象是解题的关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,为了躲避台风,一轮船一直由西向东航行,上午10点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,中午12点到达B处,并测得小岛P的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船是否能一直向东航行?
已知:如图,为了躲避台风,一轮船一直由西向东航行,上午10点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,中午12点到达B处,并测得小岛P的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船是否能一直向东航行?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com