
等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E。
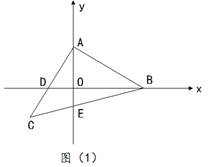
(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
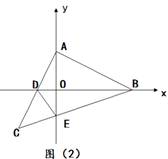
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
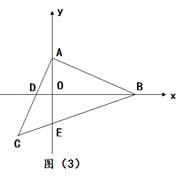
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由。
(1)C(-1,-1);(2)见解析;(3)BD=2(OA +OD)
【解析】
试题分析:(1)过点C作CF⊥y轴于点F,则△ACF≌△ABO(AAS),即得CF=OA=1,AF=OB=2,
从而求得结果;
(2)过点C作CG⊥AC交y轴于点G,则△ACG≌△ABD(ASA),即得CG=AD=CD,∠ADB=∠G, 由∠DCE=∠GCE=45°,可证△DCE≌△GCE(SAS)得∠CDE=∠G,从而得到结论;
(3)在OB上截取OH=OD,连接AH,由对称性得AD=AH, ∠ADH=∠AHD,可得∠AHD=∠ADH=∠BAO=∠BEO,即得∠AEC=∠BHA,从而证得△ACE≌△BAH(AAS),即可得到 AE=BH=2OA,从而得到结果.
(1)如图,过点C作CF⊥y轴于点F

则△ACF≌△ABO(AAS),
∴CF=OA=1,AF=OB=2
∴OF=1
∴C(-1,-1);
(2)如图,过点C作CG⊥AC交y轴于点G

则△ACG≌△ABD(ASA)
∴CG=AD=CD,∠ADB=∠G
∵∠DCE=∠GCE=45°
∴△DCE≌△GCE(SAS)
∴∠CDE=∠G
∴∠ADB=∠CDE;
(3) 如图,在OB上截取OH=OD,连接AH

由对称性得AD=AH, ∠ADH=∠AHD
∴∠AHD=∠ADH=∠BAO=∠BEO
∴∠AEC=∠BHA
又∵AB=AC ∠CAE=∠ABH
∴△ACE≌△BAH(AAS)
∴AE=BH=2OA
∵DH=2OD
∴BD=2(OA +OD)
考点:本题考查的是全等三角形的判定和性质
点评:解答本题的关键是正确作出辅助线,同时熟练掌握全等三角形的判定方法,灵活选择恰当的三角形进行分析.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
 16、如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP将线段OP绕O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP的长度等于
16、如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP将线段OP绕O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP的长度等于查看答案和解析>>
科目:初中数学 来源: 题型:
 27、如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
27、如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:
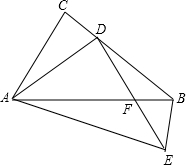 在等腰Rt△ABC中,AC=BC,点D在BC上,过点D作DE⊥AD,过点B作BE⊥AB交DE于点E,DE交AB于F.
在等腰Rt△ABC中,AC=BC,点D在BC上,过点D作DE⊥AD,过点B作BE⊥AB交DE于点E,DE交AB于F.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
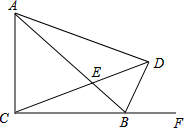 如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,
如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com