

分析 (1)先作CH⊥AB,根据等腰三角形三线合一的性质,得出AH=KH,即5-m=4m,求得m的值;
(2)先作QK⊥x轴,判定△APE≌△BQK,以及△PEG≌△QKG,得出EG=KG,根据EG=$\frac{1}{2}$EK=$\frac{1}{2}$AB进行计算即可;
(3)作MN⊥y轴于N,连接CM,先判定△MGN≌△GQK,得出GK=MN=4=CH,再根据△GCM的面积等于8,得到$\frac{1}{2}$×CM×MN=8,即2CM=8,求得CM=4,最后根据矩形MNHC中,HN=CM=2,OH=2,得到ON=OH+HN=2+4=6,进而得出M的坐标.
解答  解:(1)如图1,作CH⊥AB于H,
解:(1)如图1,作CH⊥AB于H,
∵C(2,4),A(m-3,0),B(4m+2,0),
∴AH=2-(m-3)=5-m,BH=4m+2-2=4m,
∵AC=BC,
∴AH=KH,即5-m=4m,
解得m=1;
(2)如图1,作QK⊥x轴于K,
∵PE⊥AE,
∴∠BKQ=∠AEP=90°,
∵点Q由点B出发,以与点P相同的速度沿射线CB方向运动,
∴AP=BQ,
∵AC=BC,
∴∠CAB=∠CBA=∠KBQ
在△APE和△BQK中,
$\left\{\begin{array}{l}{∠PAE=∠QBK}\\{∠AEP=∠KBQ}\\{AP=BQ}\end{array}\right.$,
∴△APE≌△BQK(AAS),
∴PE=QK,AE=KB,
在△PEG和△QKG中,
$\left\{\begin{array}{l}{∠PGE=∠QGK}\\{∠PEG=∠QKG}\\{PE=QK}\end{array}\right.$,
∴△PEG≌△QKG(AAS),
∴EG=KG,
由(1)可得,m=1,
∴AO=2,BO=6,BK=AE=1,AB=2+6=8,
∴EG=$\frac{1}{2}$EK=$\frac{1}{2}$AB=4;
(3)如图2,作MN⊥y轴于N,连接CM,
∵△PEG≌△QKG,
∴PG=QG,
又∵PM=MQ,∠PMQ=90°,MG⊥PQ,
∴∠MQP=∠MPQ=∠GMQ=∠MQG=45°,
∴MG=GQ,
∵∠GMN+∠MGB=90°=∠QGK+∠MGK,
∴∠GMN=∠QGK,
在△MGN和△GQK中,
$\left\{\begin{array}{l}{∠GMN=∠QGK}\\{∠MNG=∠GKQ}\\{MG=QG}\end{array}\right.$,
∴△MGN≌△GQK(AAS),
∴GK=MN,
又∵GK=EG=4,C(2,4),
∴MN=4=CH,
∴CM∥x轴,
∴∠MCH=∠CHE=90°,
∵△GCM的面积等于8,
∴$\frac{1}{2}$×CM×MN=8,即2CM=8,
∴CM=4,
∴矩形MNHC中,HN=CM=2,
又∵OH=2,
∴ON=OH+HN=2+4=6,
∴M(6,4).
点评 本题主要考查了三角形的综合应用,解决问题时需要运用等腰三角形的性质、全等三角形的判定与性质、三角形的面积计算公式以及矩形的性质等,解题时注意:两角及其中一个角的对边对应相等的两个三角形全等,全等三角形的对应边相等.解决问题的关键是作辅助线构造全等三角形以及矩形.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
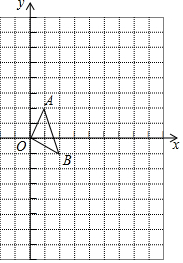 如图,在正方形网格中,每一个小正方形的边长都为1,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
如图,在正方形网格中,每一个小正方形的边长都为1,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com