
【题目】根据下列数量关系列不等式:
(1)a与1的和是正数 ;
(2)a的![]() 和b的
和b的![]() 的差是负数 ;
的差是负数 ;
(3)a与b的两数和的平方不大于9 ;
(4)a的![]() 倍与b的和的平方是非负数 .
倍与b的和的平方是非负数 .
科目:初中数学 来源: 题型:
【题目】某小区将原来400平方米的正方形场地改建成300平方米的长方形场地,且长和宽之比为3∶2.如果把原来正方形场地的铁栅栏围墙利用起来围成新场地的长方形围墙,那么这些铁栅栏是否够用?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN= ![]() AB,求折痕MN的长;
AB,求折痕MN的长;
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.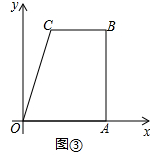
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.

(1)求证:AE=AF;
(2)求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与双曲线y= ![]() (x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C. 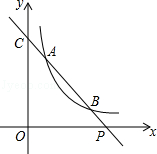
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1 , x2 , x0之间的关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧 ![]() 上的点F作FH⊥AD于点H,且FH=1.5
上的点F作FH⊥AD于点H,且FH=1.5
(1)求点D的坐标及该抛物线的表达式;
(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD//BC和AB//CD.请完成下面的推理过程,填写理由或数学式:

∵∠1=∠2,∠1=∠AGH(_________)
∴∠2=∠AGH(________)
∴AD//BC(________)
∴∠ADE=∠C(________)
∵∠A=∠C(已知)
∴∠ADE=_______(等量代换)
∴AB//CD(_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
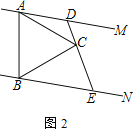
【题目】已知,在![]() 中,
中,![]() ,分别过
,分别过![]() 、
、![]() 点作互相平行的直线
点作互相平行的直线![]() 、
、![]() ,过点
,过点![]() 的直线分别交直线
的直线分别交直线![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)![]() ;
;
① 若![]() ,直接写出
,直接写出![]() 、
、![]() 的数量关系;
的数量关系;
② 如图1,![]() 与
与![]() 不垂直,判断上述结论是否还成立,并说明理由;
不垂直,判断上述结论是否还成立,并说明理由;
(2)如图2,![]() ,
,![]() ,
,![]() ,求
,求![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com