
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为底边作等腰三角形
为底边作等腰三角形![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上的一点,则当点
上的一点,则当点![]() 为何处时,
为何处时,![]() 的周长最小,并求出此时
的周长最小,并求出此时![]() 的周长.
的周长.
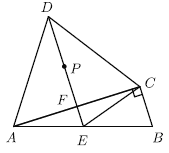
【答案】(1)证明见解析.(2)![]() .
.
【解析】
(1)首先证明EA=EC,再证明EC=EB即可解决问题.
(2)先说明P与E重合时△PBC的周长最小,最小值=AB+AC.
(1)证明:∵DA=DC,DF⊥AC,
∴AF=CF,
∴DE垂直平分线段AC,
∴EA=EC,
∴∠EAC=∠ECA,
∵∠ACB=90°,
∴∠EAC+∠B=90°,∠ECA+∠ECB=90°,
∴∠ECB=∠B,
∴EC=EB=EA.
(2)连接PB、PC、PA.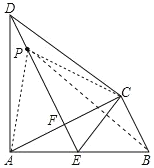
要使得△PBC的周长最小,只要PB+PC最小即可.
∵PB+PC=PA+PB≥AB,
∴当P与E重合时,PA+PB最小,
∴△PBC的周长最小值=AB+BC=15+9=24cm.


科目:初中数学 来源: 题型:
【题目】画图题:(不写画法)
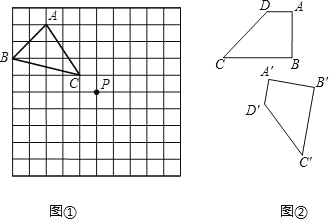
(1)如图①,在 10×10 的正方形网格中,每个小正方形的边长为1个单位. 请作出△ABC 绕点P逆时针旋转 90°的△A′B′C′;
(2)如图②,四边形A′B′C′D′是由四边形ABCD绕某一点旋转得到的,请通过作图确定这个点,并把它命名为点O,再把四边形ABCD关于点O的中心对称图形A′B′C′D′画出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山居民(记为C)、李庄古镇(记为D)中的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为________;
(2)用画树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位。那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似。
例如计算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ 。
_________ 。
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求![]() 的值。
的值。
(4)试一试:请利用以前学习的有关知识将![]() 化简成
化简成![]() 的形式。
的形式。
(5)解方程:x2 - 2x +4 = 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题成立的是( ).
A.全等三角形的对应角相等
B.若三角形的三边满足![]() ,则该三角形是直角三角形
,则该三角形是直角三角形
C.对顶角相等
D.同位角互补,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .一次函数的图象分别交
.一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
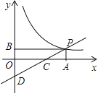
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式:
(3)根据图象写出当![]() 时,一次函数的值小于反比例函数的值的
时,一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线y=ax+b与直线y=bx+a互为“友好直线”.如:直线y=2x+1与直线y=x+2互为“友好直线”.
(1)点M(m,2)在直线y=-x+4的“友好直线”上,则m=________;
(2)直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点,求点M的坐标;
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上,求直线y=ax+b的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将![]() 个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
![]() 补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
![]() 估算袋中白球的个数;
估算袋中白球的个数;
![]() 在
在![]() 的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com