
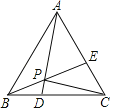
【题目】如图所示,等边△ABC的边长为4,点D是BC边上一动点,且CE=BD,连接AD,BE,AD与BE相交于点P,连接PC.则线段PC的最小值等于_____.
【答案】![]()
【解析】
由“SAS”可证△ABD△BCE,可得∠BAD=∠CBE,由此进一步可求∠APB=120°,据此如图,作等腰△AOB,使OA=OB,∠AOB=120°,连接OC,OP,可得点P在以点O为圆心,OB为半径的圆上,当点O,点P,点C共线时,PC有最小值,最后利用直角三角形的性质进一步求解即可.
∵△ABC是等边三角形,
∴AB=AC=BC=4,∠ABC=∠BAC=∠ACB=60°,
∵CE=BD,∠ABC=∠BCE=60°,AB=BC,
∴△ABD△BCE(SAS)
∴∠BAD=∠CBE,
∵∠ABP+∠CBP=∠ABC=60°,
∴∠ABP+∠BAD=60°,
∴∠APB=120°,
如图:作等腰△AOB,使OA=OB,∠AOB=120°,连接OC,OP,

∵∠APB=120°,
∴点P在以点O为圆心,OB为半径的圆上,
∵CP≥OCOP,
∴当点O,点P,点C共线时,PC有最小值,
∵OA=OB,∠AOB=120°,
∴∠ABO=30°,
∴∠CBO=90°,
∵OA=OB,BC=CA,OC=OC,
∴△AOC△BOC(SSS),
∴∠ACO=∠BCO=30°,
∴CO=2OB,
∵OC2OB2=BC2,
∴3OB2=16
∴OB=![]() ,
,
∴OC=![]()
∴PC的最小值=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
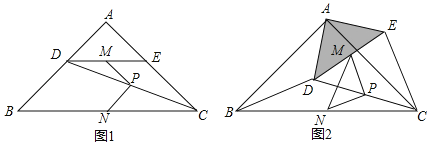
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.1 |
70≤x<80 | 90 | n |
80≤x<90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |

请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)在表中:m= .n= ;
(3)补全频数分布直方图:
(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在 分数段内;
(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB∥x轴,AB=6.点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点G是AD与y轴的交点,点P是CD边上不与点C,D重合的一个动点,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+4x+5图象的顶点为D,对称轴是直线1,一次函数y![]() x+1的图象与x轴交于点A,且与直线DA关于l的对称直线交于点B.
x+1的图象与x轴交于点A,且与直线DA关于l的对称直线交于点B.
(1)点D的坐标是 ;
(2)直线l与直线AB交于点C,N是线段DC上一点(不与点D、C重合),点N的纵坐标为n.过点N作直线与线段DA、DB分别交于点P、Q,使得△DPQ与△DAB相似.
①当n![]() 时,求DP的长;
时,求DP的长;
②若对于每一个确定的n的值,有且只有一个△DPQ与△DAB相似,请直接写出n的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )


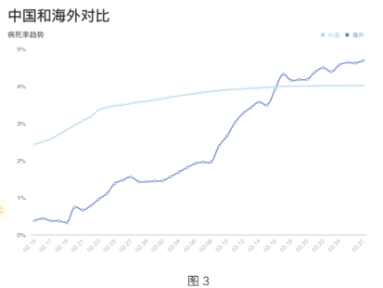
A.图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量.
B.图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半.
C.图2显示意大利当前的治愈率高于西班牙.
D.图3显示大约从3月16日开始海外的病死率开始高于中国的病死率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 交于点
交于点![]() ,将点
,将点![]() 向右平移某个距离得到点
向右平移某个距离得到点![]() ,点
,点![]() 在抛物线上.已知点
在抛物线上.已知点![]() ,
,![]() .
.
(1) 当![]() 时.
时.
①求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
②求线段![]() 的长度;
的长度;
(2)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
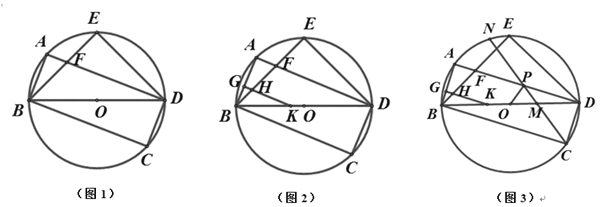
【题目】已知:矩形ABCD内接于⊙O,连接 BD,点E在⊙O上,连接 BE交 AD于点F,∠BDC+45°=∠BFD,连接ED.
(1)如图 1,求证:∠EBD=∠EDB;
(2)如图2,点G是 AB上一点,过点G作 AB的垂线分别交BE和 BD于点H和点K,若HK=BG+AF,求证:AB=KG;
(3)如图 3,在(2)的条件下,⊙O上有一点N,连接 CN分别交BD和 AD于![]() 点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产并销售A,B两种品牌新型节能设备,第一季度共生产两种品牌设备20台,每台的成本和售价如下表:
品牌 | A | B |
成本价(万元/台) | 3 | 5 |
销售价(万元/台) | 4 | 8 |
设销售A种品牌设备x台,20台A,B两种品牌设备全部售完后获得利润y万元.(利润=销售价-成本)
(1)求y关于x的函数关系式;
(2)若生产两种品牌设备的总成本不超过80万元,那么公司如何安排生产A,B两种品牌设备,售完后获利最多?并求出最大利润;
(3)公司为营销人员制定奖励促销政策:第一季度奖金=公司总利润![]() 销售A种品牌设备台数
销售A种品牌设备台数![]() ,那么营销人员销售多少台A种品牌设备,获得奖励最多?最大奖金数是多少?
,那么营销人员销售多少台A种品牌设备,获得奖励最多?最大奖金数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com