
 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为 (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.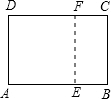

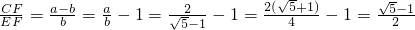
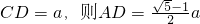 ,
,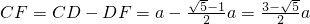
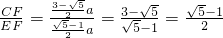


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 若一个矩形的短边与长边的比值为
若一个矩形的短边与长边的比值为
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 我们已经知道,如果线段MN被点P分成线段MP和PN,且
我们已经知道,如果线段MN被点P分成线段MP和PN,且| MP |
| MN |
| PN |
| MP |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012届浙江省宁波市九年级中考适应性考试(一)数学卷(带解析) 题型:解答题
若一个矩形的短边与长边的比值为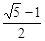 (黄金分割数),我们把这样的矩形叫做黄金矩形.
(黄金分割数),我们把这样的矩形叫做黄金矩形.
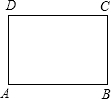
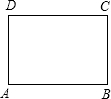
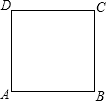
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com