
【题目】已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.

(1)求点B的坐标;
(2)在x轴上找一点D,连接BD使得△ABD与△ABC相似(不包括全等),并求点D的坐标.
【答案】(1) B点坐标为(1,3);(2) D(![]() ,0)
,0)
【解析】
(1)根据点A、C的坐标求出AC的长度,再根据tan∠BAC=![]() 求出BC的长度,然后即可写出点B的坐标;
求出BC的长度,然后即可写出点B的坐标;
(2)过点B作BD⊥AB,交x轴于点D,D点为所求.又tan∠ADB=tan∠ABC=![]() ,CD=BC÷tan∠ADB=3÷
,CD=BC÷tan∠ADB=3÷![]() =
=![]() ,可求OD=OC+CD=
,可求OD=OC+CD=![]() ,所以D(
,所以D(![]() ,0).
,0).
(1)∵点A(﹣3,0),C(1,0),
∴AC=4,
则BC=tan∠BAC×AC=![]() ×4=3,
×4=3,
∴B点坐标为(1,3),
(2)如图,过点B作BD⊥AB,交x轴于点D,

在Rt△ABC和Rt△ADB中,
∵∠BAC=∠DAB,
∴Rt△ABC∽Rt△ADB,
∴D点为所求,
又tan∠ADB=tan∠ABC=![]() ,
,
∴CD=BC÷tan∠ADB=3÷![]() =
=![]() ,
,
∴OD=OC+CD=![]() ,
,
∴D(![]() ,0).
,0).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】体育器材室有A、B两种型号的实心球,1只A型球与1只B型球的质量共7千克,3只A型球与1只B型球的质量共13千克.
(1)每只A型球、B型球的质量分别是多少千克?
(2)现有A型球、B型球的质量共17千克,则A型球、B型球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)小敏在学习了Rt△ABC的性质定理后,继续进行研究.
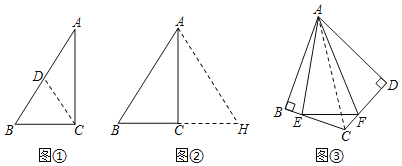
(1)(i)她发现图①中,如果∠A=30°,BC与AB存在特殊的数量关系是 ;
(ii)她将△ABC沿AC所在的直线翻折得△AHC,如图②,此时她证明了BC和AB的关系;请根据小敏证明的思路,补全探究的证明过程;
猜想:如果∠A=30°,BC与AB存在特殊的数量关系是 ;
证明:△ABC沿AC所在的直线翻折得△AHC,
(2)如图③,点E、F分别在四边形ABCD的边BC、CD上,且∠B=∠D=90°,连接AE、AF、EF,将△ABE、△ADF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形,连接AC,若∠EAF=30°,AB2=27,则△CEF的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用![]() 元购进某款智能清洁机器人进行销售,很快销售一空,商家又用
元购进某款智能清洁机器人进行销售,很快销售一空,商家又用![]() 元第二次购进同款智能清洁机器人,所购进数量是第一次的
元第二次购进同款智能清洁机器人,所购进数量是第一次的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.
元.
(1)求该商家第一次购进智能清洁机器人多少台?
(2)若所有智能清洁机器人都按相同的标价销售,要求全部销售完毕的利润率不低于![]() (不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
(不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )
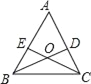
A. 5对 B. 6对 C. 7对 D. 8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
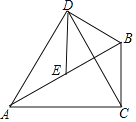
(1)求证:△ADE≌△CDB;
(2)若BC=1,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com