
为了预防“感冒”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后y与x成反比例如图。现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为___,自变量x的取值范围是___;药物燃烧后y关于x的函数关系式为___.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过___分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病毒,那么此次消毒有效吗?为什么?
(1)药物燃烧时y关于x的函数关系式为y=x(0?x?8)药物燃烧后y关于x的函数关系式为y= (x>8)(2)从消毒开始,至少需要30分钟后学生才能进入教室(3)这次消毒是有效的 【解析】试题分析:(1)药物燃烧时,设出y与x之间的解析式y=k1x,把点(8,6)代入即可,从图上读出x的取值范围;药物燃烧后,设出y与x之间的解析式,把点(8,6)代入即可; (2)把y=1.6代入反比...科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:解答题
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:解答题
在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画出所有符合条件的整点三角形.
(1)在图1中画△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.

查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:单选题
在平面直角坐标系中,点P(﹣1,2)的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B 【解析】 试题分析:本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).∵点P(﹣1,2)的横坐标﹣1<0,纵坐标2>0,∴点P在第二象限.查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:单选题
下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
A. a= ,b=
,b=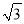 ,c=
,c= B. a=1.5,b=2,c=3
B. a=1.5,b=2,c=3
C. a=6,b=8,c=10 D. a=3,b=4,c=5
B 【解析】根据勾股定理的逆定理对各选项进行逐一判断即可. 【解析】 A、∵,∴能构成直角三角形,故本选项不符合题意; B、∵1.52+22=6.25≠32,∴不能构成直角三角形,故本选项符合题意; C、∵62+82=100=102,∴能构成直角三角形,故本选项不符合题意; D、∵32+42=25=52,∴能构成直角三角形,故本选项不符合题意. 故选B. “点睛”本题考...查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:填空题
一个底面直径是80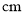 ,母线长为
,母线长为 的圆锥的侧面展开图的圆心角的度数为______ 。
的圆锥的侧面展开图的圆心角的度数为______ 。
查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:单选题
如图,在平面直角坐标系 中,半径为2的
中,半径为2的 的圆心P的坐标为(-3,0),将
的圆心P的坐标为(-3,0),将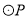 沿x轴正方向平移,使
沿x轴正方向平移,使 与
与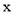 轴相切,则平移的距离为( )
轴相切,则平移的距离为( )

A. 1 B. 1或5 C. 3 D. 5
B 【解析】试题分析:当⊙P位于y轴的左侧且与y轴相切时,平移的距离为1; 当⊙P位于y轴的右侧且与y轴相切时,平移的距离为5. 故选B.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十九章达标检测卷 题型:填空题
如果一次函数y=(k﹣2)x+1的图象经过一、二、三象限,那么常数k的取值范围是______.
k>2; 【解析】根据一次函数图像与性质,可知图像过一、二、三象限时,k-2>0,解得k>2. 故答案为:k>2.查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
求证:(1)BD=CE;(2)∠M=∠N.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com