
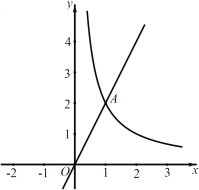
【题目】如图,直线![]() 与函数
与函数![]()
![]() 的图象交于点
的图象交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与函数
,与函数![]()
![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
①若点![]() 是线段
是线段![]() 的中点时,则点
的中点时,则点![]() 的坐标是______,
的坐标是______,![]() 的值是______;(直接写答案)
的值是______;(直接写答案)
②当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)①![]() ,-3;②
,-3;②![]()
【解析】
(1)根据待定系数法求解即可;
(2)①根据题意求得C点的坐标,然后根据待定系数法即可求得b的值;②根据①结合图象即可求解.
解:(1)把![]() (1,2)代入函数
(1,2)代入函数![]()
![]() 中,
中,
∴![]() ,
,
∴![]() .
.
(2))①过点C作x轴的垂线,交直线l于点E,交x轴于点F,
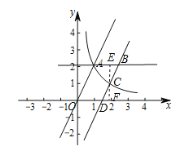
∵点C是线段BD的中点时,
∴点C的纵坐标为1,
将![]() 代入函数
代入函数![]() 中,得
中,得![]() ,
,
∴点C的坐标为(2,1),
将C(2,1)代入函数![]() 中,得
中,得![]() ,
,
②当C在AB的上方时,如图过点B作MB垂直于x轴于点M,过点C作CN垂直于MB于点N,
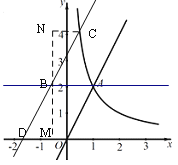
当![]() 时,易证
时,易证![]() ,
,
则![]() ,
,
∴点N的纵坐标为4,
把![]() 代入函数
代入函数![]() 中,得
中,得![]() ,
,
∴点C的坐标为(![]() ,4),
,4),
把点C代入函数![]() 中,得
中,得![]() ,
,
∴当![]() 时,
时,![]() ,
,
故b的取值范围为:![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形 ABCD的两条对角线相交于点O, E是BO的中点.过B点作AC的平行线,交CE的延长线于点F,连接BF.
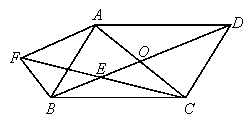
(1)求证:FB=AO;
(2)当平行四边形 ABCD满足什么条件时,四边形AFBO是菱形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制成如下统计图表(单位:cm):
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
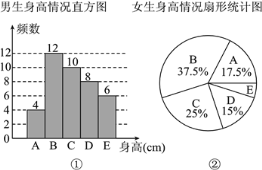
根据图表提供的信息,样本中,身高在160≤x<170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() ),其对称轴是
),其对称轴是![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() ,
,![]() 之间.有下列结论:①
之间.有下列结论:①![]() ;②
;②![]() ;③若此抛物线过
;③若此抛物线过![]() 和
和![]() 两点,则
两点,则![]() ,其中,正确结论的个数为( )
,其中,正确结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数,
为常数,![]() 与
与![]() 合起来的图象记为
合起来的图象记为![]() .
.
(Ⅰ)若![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)若![]() 的顶点在直线
的顶点在直线![]() 上,求
上,求![]() 的值;
的值;
(Ⅲ)设![]() 在
在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求该抛物线的函数表达式及对称轴;
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点),如果直线
两点),如果直线![]() 与图象
与图象![]() 有一个公共点,结合函数的图象,直接写出点
有一个公共点,结合函数的图象,直接写出点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情防控期间.某小区卫生所决定购买A,B两种口罩.以满足小区居民的需要.若购买A种口罩9包,B种口罩4包,则需要700元;若购买A种口罩3包.B种口罩5包.则需要380元.
(1)购买人A,B两种口罩每包各需名少元?
(2)卫生所准备购进这两种口罩共90包,并且A种口罩包数不少于B种口罩包数的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 分别与x轴,y轴交于点
分别与x轴,y轴交于点![]() ,点C是第一象限内的一点,且
,点C是第一象限内的一点,且![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与x轴的另一交点为D.
两点,与x轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以![]() 四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
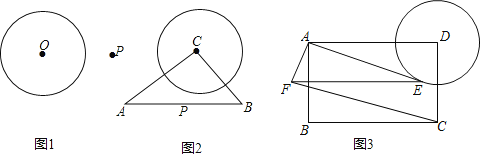
【题目】(1)如图1,A是⊙O上一动点,P是⊙O外一点,在图中作出PA最小时的点A.
(2)如图2,Rt△ABC中,∠C=90°,AC=8,BC=6,以点C为圆心的⊙C的半径是3.6,Q是⊙C上一动点,在线段AB上确定点P的位置,使PQ的长最小,并求出其最小值.
(3)如图3,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,∠EAF=90°,tan∠AEF=![]() ,试探究四边形ADCF的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
,试探究四边形ADCF的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com