
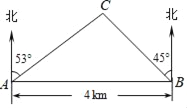
【题目】如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东53°方向上,从B测得灯塔C在北偏西45°方向上,求灯塔C与观测点A的距离(精确到0.1km).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
【答案】灯塔C与观测点A的距离为2.9km.
【解析】
如图,过点C作CD⊥AB,构建直角△ACD和直角△BCD.通过解Rt△ADC得到AD=ACcos37°,CD=ACsin37°,通过解Rt△BDC得到BD=CD.所以由AB=AD+DB来求AC的长度.
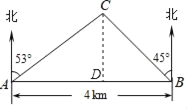
解:如图,作CD⊥AB,垂足为D.
由题意可知:∠CAB=90°﹣53°=37°,
∠CBA=90°﹣45°=45°,
∴在Rt△ADC中,
cos∠CAB=![]() ,即AD=ACcos37°;
,即AD=ACcos37°;
sin∠CAB=![]() ,即CD=ACsin37°.
,即CD=ACsin37°.
在Rt△BDC中,tan∠CBA=![]() ,即BD=
,即BD=![]() =CD.
=CD.
∵AB=AD+DB,
∴ACcos37°+ACsin37°=4.
∴AC=![]() ≈2.9km.
≈2.9km.
答:灯塔C与观测点A的距离为2.9km.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
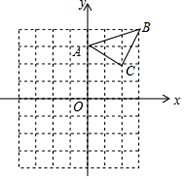
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
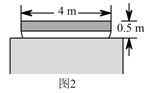
【题目】河上有一座桥孔为抛物线形的拱桥(如图 ![]() ),水面宽
),水面宽 ![]() 时,水面离桥孔顶部
时,水面离桥孔顶部 ![]() ,因降暴雨水面上升
,因降暴雨水面上升 ![]() .
.
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
(2)一艘装满物资的小船,露出水面的部分高为 ![]() ,宽
,宽 ![]() (横断面如图
(横断面如图 ![]() 所示),暴雨后这艘船能从这座拱桥下通过吗?
所示),暴雨后这艘船能从这座拱桥下通过吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
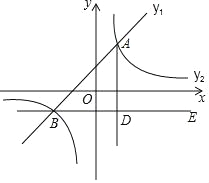
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象交于点A(1,2)和B(﹣2,m).
的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1≥y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若∠DAC=30°,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC绕O点逆时针旋转90°得到△A1B1C1,请画出△A1B1C1.
(2)在x轴上求作一点P,使△PA1C1的周长最小,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西贺州市)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果中的牛油果和桔子的维生素含量很高,因此深受人们喜爱,“农夫果园”水果商家11月份购进了第一批牛油果和桔子共300千克,已知牛油果进价每千克15元,售价每千克30元,桔子进价每千克5元,售价每千克10元.
(1)若这批牛油果和桔子全部销售完获利不低于3500元,则牛油果至少购进多少千克?
(2)第一批牛油果和桔子很快售完,于是商家决定购进第二批牛油果和桔子,牛油果和桔子的进价不变,牛油果售价比第一批上涨a%(其中a为正整数),桔子售价比第一批上涨2a%;销量与(1)中获得最低利润时的销量相比,牛油果的销量下降a%,桔子的销量保持不变,结果第二批中已经卖掉的牛油果和桔子的销售总额比(1)中第一批牛油果和桔子销售完后对应最低销售总额增加了2%,求正整数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
与x轴交于A、B两点,与y轴交于点C,顶点为D,连接BC
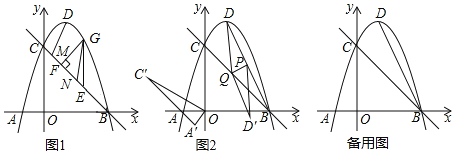
![]() 点G是直线BC上方抛物线上一动点
点G是直线BC上方抛物线上一动点![]() 不与B、C重合
不与B、C重合![]() ,过点G作y轴的平行线交直线BC于点E,作
,过点G作y轴的平行线交直线BC于点E,作![]() 于点F,点M、N是线段BC上两个动点,且
于点F,点M、N是线段BC上两个动点,且![]() ,连接DM、
,连接DM、![]() 当
当![]() 的周长最大时,求
的周长最大时,求![]() 的最小值;
的最小值;
![]() 如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将
如图2,连接BD,点P是线段BD的中点,点Q是线段BC上一动点,连接DQ,将![]() 沿PQ翻折,且线段
沿PQ翻折,且线段![]() 的中点恰好落在线段BQ上,将
的中点恰好落在线段BQ上,将![]() 绕点O逆时针旋转
绕点O逆时针旋转![]() 得到
得到![]() ,点T为坐标平面内一点,当以点Q、
,点T为坐标平面内一点,当以点Q、![]() 、
、![]() 、T为顶点的四边形是平行四边形时,求点T的坐标.
、T为顶点的四边形是平行四边形时,求点T的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
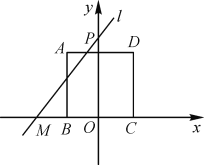
【题目】如图,正方形ABCD的边长为2,BC边在x轴上,BC的中点与原点O重合,过定点M(-2,0)与动点P(0,t)的直线MP记作l.
(1)若l的解析式为y=2x+4,判断此时点A是否在直线l上,并说明理由;
(2)当直线l与AD边有公共点时,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com