
【题目】如图1,平面直角坐标系中,抛物线y= ![]() 与x 轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.
与x 轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.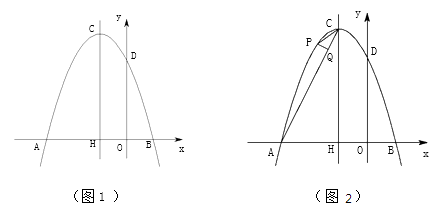
(1)求抛物线的表达式;
(2)点E,F 分别是抛物线对称轴CH 上的两个动点(点E 在点F 上方),且EF=1,求使四边形BDEF 的周长最小时的点E,F 坐标及最小值;
(3)如图2,点P 为对称轴左侧,x 轴上方的抛物线上的点,PQ⊥AC 交AC 于点Q,是否存在这样的点P 使△PCQ与△ACH 相似,若存在请求出点P 的坐标,若不存在请说明理由.
【答案】
(1)
将A(﹣3,0)、B(1,0),代入y=ax2+bx+3,
得: ![]()
解得:![]()
抛物线的解析式为:y=﹣x2﹣2x+3,
顶点C的坐标为(﹣1,4).
(2)
将D点向下平移1个单位,得点M,连接AM交对称轴于F,作DE∥FM交对称轴于E点,
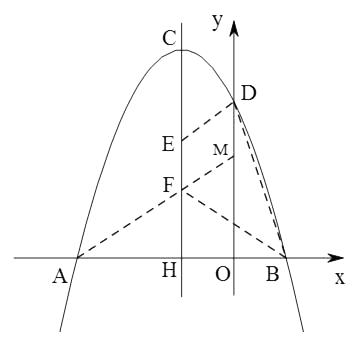
如图,EF∥DM,DE∥FM,四边形EFMD是平行四边形,
DE=FM,EF=DM=1.
DE+FB=FM+AF=AM.
由勾股定理,得AM=![]() =
=![]() ,
,
BD= ![]()
四边形BDEF周长的最小值=BD+DE+EF+FB
=BD+EF+(DE+BF)
= BD+EF +AM
=![]() +1+
+1+![]() ;
;
设AM的解析式为y=kx+b,将A、M点坐标代入解得k=![]() ,b=2.
,b=2.
AD的解析式为y= ![]() x+2,
x+2,
当x=﹣1时,y=![]() ,即F(﹣1,
,即F(﹣1, ![]() ),
),
由EF=1,得E(﹣1,![]() ),
),
当四边形BDEF周长最小时,此时点F(﹣1, ![]() ),E的坐标(﹣1,
),E的坐标(﹣1, ![]() ),
),
四边形BDEF周长的最小值是![]() +1+
+1+![]() .
.
(3)
点P在对称轴左侧.
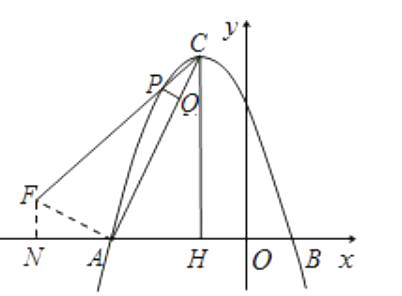
只能是△PCQ∽△ACH,得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F,作FN⊥x轴于点N.
由△CFA∽△CAH得 ![]() =2,
=2,
由△FNA∽△AHC得 ![]() .
.
∴AN=2,FN=1,点F坐标为(﹣5,1).
设直线CF的解析式为y=k2x+b2,则![]() ,
,
解得: 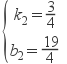 .
.
∴直线CF的解析式 ![]() ,
,
联立  ,
,
解得: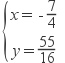 或 (舍去)
或 (舍去)![]() .
.
∴满足条件的点P坐标为 ![]() .
.
【解析】(1)二次函数解析系中有2个未知数,所以就需要2个点,将两点的坐标代进去即可求得;
(2)根据轴对称-求最短路径的方法去做;
(3)因为∠PCQ<∠CAH,所以只能是△PCQ∽△ACH,得∠PCQ=∠ACH.过A作CA的垂线交PC于点F,作FN⊥x轴于点N.


科目:初中数学 来源: 题型:
【题目】某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
时间t(天) | 1 | 3 | 5 | 10 | 36 | … |
日销售量m(件) | 94 | 90 | 86 | 76 | 24 | … |
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1= ![]() t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣
t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣ ![]() t+40(21≤t≤40且t为整数).
t+40(21≤t≤40且t为整数).
下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的表达式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( ) 
A.(4,3)
B.(5, ![]() )
)
C.(4, ![]() )
)
D.(5,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).
(1)当t为何值时,PQ∥BC.
(2)设△AQP的面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b 的图象l与坐标轴分别交于点E、F,与双曲线y=- ![]() (x<0)(x<0)交于点P(﹣1,n),且F 是PE 的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a=。
(x<0)(x<0)交于点P(﹣1,n),且F 是PE 的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a=。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论: ①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);
④若点(m,n)在反比例函数y= ![]() 的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A.①②
B.③④
C.②③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 , 位置关系是;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: y= ![]() .
.
(1)李明第几天生产的粽子数量为420只?
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本)
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com