
分析 根据角平分线定理得到比例式:$\frac{AB}{BC}=\frac{AD}{CD}$①,$\frac{AC}{BC}=\frac{AE}{BE}$,由于BE=CD,得到$\frac{AC}{BC}=\frac{AE}{CD}$②,①÷②得:$\frac{AB}{AC}=\frac{AD}{AE}=\frac{AC-CD}{AB-BE}$=$\frac{AC-CD}{AB-CD}$,化简得(AB-AC)(AB+AC-CD)=0,由于AB+AC-CD≠0,得到AB-AC=0,于是得到结论.
解答  证明:∵BD、CE分别是∠ABC、∠ACB的角平分线,
证明:∵BD、CE分别是∠ABC、∠ACB的角平分线,
∴$\frac{AB}{BC}=\frac{AD}{CD}$ ①,$\frac{AC}{BC}=\frac{AE}{BE}$,
∵BE=CD,
∴$\frac{AC}{BC}=\frac{AE}{CD}$ ②,
①÷②得:$\frac{AB}{AC}=\frac{AD}{AE}=\frac{AC-CD}{AB-BE}$=$\frac{AC-CD}{AB-CD}$,
∴AB2-AB•CD=AC2-AC•CD,
∴AB2-AC2=(AB-CD)•CD,
化简得(AB-AC)(AB+AC-CD)=0,
∵AB+AC-CD≠0,
∴AB-AC=0,
即AB=AC.
点评 本题考查了角平分线定理,因式分解,熟练掌握角平分线定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | h≥-2 | B. | h≤-2 | C. | h>-2 | D. | h<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
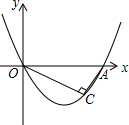 如图,抛物线y=$\frac{1}{2}$x2-$\frac{5}{2}$x与x轴交于O、A两点,点C为第四象限的抛物线上一点,且OC⊥AC,求点C的坐标.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{5}{2}$x与x轴交于O、A两点,点C为第四象限的抛物线上一点,且OC⊥AC,求点C的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{-a+b}{a-b}$=-1 | B. | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | C. | $\frac{2a-b}{2a+b}$=$\frac{a-b}{a+b}$ | D. | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a+b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com