
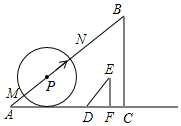
 游歌乐山森林公园最佳路线推荐:如图,先从A沿登山步道走到C,再乘坐索道缆车到B,已知在A处观测B,测得仰角∠FAB=31°,且A,C的水平距离AD=150米,A,C的竖直距离CD=40米,索道BC的坡度i=2:3,则索道BC的长约为(参考数据:sin31°≈0.5,tan31°≈0.6,$\sqrt{13}$≈3.6)( )
游歌乐山森林公园最佳路线推荐:如图,先从A沿登山步道走到C,再乘坐索道缆车到B,已知在A处观测B,测得仰角∠FAB=31°,且A,C的水平距离AD=150米,A,C的竖直距离CD=40米,索道BC的坡度i=2:3,则索道BC的长约为(参考数据:sin31°≈0.5,tan31°≈0.6,$\sqrt{13}$≈3.6)( )| A. | 1200 | B. | 1100 | C. | 1000 | D. | 900 |
分析 根据索道BC的坡度i=2:3可设BE=2x,则CE=3x,再由BF⊥AF,CD⊥AF,CE⊥BF可知四边形CDFE是矩形,故可得出EF=CD=40米,CE=DF=3x,再由锐角三角函数的定义可得出x的值,进而可得出BE与CE的长,根据勾股定理可得出BC的长.
解答 解:∵索道BC的坡度i=2:3,
∴设BE=2x,则CE=3x.
∵BF⊥AF,CD⊥AF,CE⊥BF,CD=40米,AD=150米,
∴EF=CD=40米,CE=DF=3x,
∴BF=BE+EF=(2x+40)米,AF=DF+AD=(3x+150)米,
∵∠FAB=31°,
∴$\frac{BF}{AF}$=tan31°,即$\frac{2x+40}{3x+150}$=0.6,解得x=250米,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{4{x}^{2}+9{x}^{2}}$=$\sqrt{13}$x≈3.6×250=900(米).
故选D.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 11.5%+7%=x | B. | (1+11.5%)(1+7%)=2(1+x) | ||
| C. | 11.5%+7%=2x | D. | (1+11.5%)(1+7%)=(1+x)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查“神舟八号”飞船各零部件的质量 | |
| B. | 企业招聘时,对应聘人员进行面试 | |
| C. | 调查我市中学生每天体育锻炼的时间 | |
| D. | 调查2012年伦敦20届奥运会100米参赛运动 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60c,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿C方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中,
如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60c,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿C方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 每位考生的数学成绩是个体 | B. | 近35000名考生是总体 | ||
| C. | 这1000名考生是总体的一个样本 | D. | 1000名考生是样本容量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com