Question

已知，A（3，a）是双曲线y=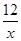 上的点，O是原点，延长线段AO交双曲线于另一点B，又过B点作BK⊥x轴于K．
（1）试求a的值与点B坐标；
（2）在直角坐标系中，先使线段AB沿x轴的正方向平移6个单位，得线段A₁B₁，再依次在与y轴平行的方向上进行第二次平移，得线段A₂B₂，且可知两次平移中线段AB先后滑过的面积相等（即?AA₁B₁B与?A₁A₂B₂B₁的面积相等）．求出满足条件的点A₂的坐标，并说明△AA₁A₂与△OBK是否相似的理由；
（3）设线段AB中点为M，又如果使线段AB与双曲线一起移动，且AB在平移时，M点始终在抛物线y= 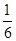（x-6）²-6上，试判断线段AB在平移的过程中，动点A所在的函数图象的解析式；（无需过程，直接写出结果．）
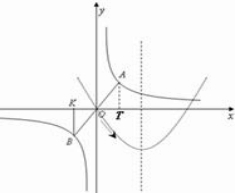
（4）试探究：在（3）基础上，如果线段AB按如图2所示方向滑过的面积为24个平方单位，且M点始终在直线x=6的左侧，试求此时线段AB所在直线与x轴交点的坐标，以及M点的横坐标．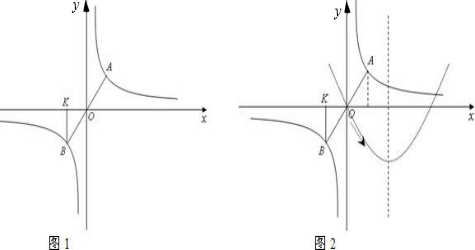

Answer 1

解：解：（1）将A代入双曲线y=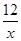中，可得3=，
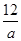故a=4，A（3，4）；由于A、B关于原点对称，那么B（-3，-4）．     
（2）∵A（3，4），B（-3，-4），则AB间的横向距离、纵向距离分别为6、8个单位，
∴由题意可得：?AA₁B₁B的面积为48，
又∵?AA₁B₁B与?A₁A₂B₂B₁的面积相等，
∴第二次线段A₁B₁进一步在纵向平移了8个单位．
故：AA₁=6，A₁A₂=8
可知，第二次在平移的方向上可能向上，也可能向下．
∴①当线段向上平移时：A（3，4）→A₁（9，4）→A₂（9，12）；
②当线段向下平移时：A（3，4）→A₁（9，4）→A₂（9，-4）．
所以A₂的坐标为：（9，12）或（9，-4）                      
又∵OK=3，KB=4，
∴
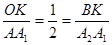
而∠OKB=∠AA₁A₂=90°，
故：△AA₁A₂∽△OBK．        
（3）由题意可知：将抛物线y=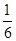（x-6）²-6向右平移3个单位，再向上平移4个单位，得：
A点满足的解析式为：y=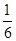（x-9）²-2．    
（4）∵AB=10且使线段AB按如图所示方向滑过的面积为24个平方单位，M在直线x=6的左侧，
∴AB在平移前后的平行距离为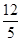
过A（3，4）点作AT⊥x轴于T，又可得T点到平移前线段AB的距离为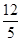

∴平移后AB直线与x轴的交点必为T（3，0）．又可知平移后AB直线解析式为：y=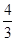x-4，
此时M为抛物线：y=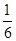（x-6）²-6与直线：y=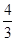x-4的交点，
∴解方程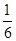：（x-6）²-6=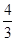x-4，
得：x=10±2
又∵0＜x＜6，
∴x=10-2，
故M的横坐标为10-2         

解析（1）将A点坐标代入反比例函数的解析式中，即可求得a的值，而A、B关于原点对称，由此求出B点的坐标．
（2）根据A、B的坐标知：A、B的横向、纵向距离分别为6、8，若线段AB向x轴正方向移动6个单位，那么它的面积应该是6×8=48，由于?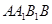与?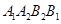的面积相等，而A、B的横距离为6，那么第二次平移的距离必为8个单位，然后分向上、向下平移两种情况分类讨论即可得到点A2的坐标；
在求△与△OBK是否相似，已知∠OKB=∠=90°，只需比较两组直角边是否对应成比例即可．
（3）已知了M、A的横、纵坐标的差分别为3、4，因此将过M的抛物线向右平移3个单位后，再向上平移4个单位，即可得到所求的抛物线解析式．
（4）易知AB=10，若平移后扫过的面积为24，那么线段AB平行移动的距离为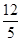,过A作x轴的垂线，设垂足为T，则T到AB的距离为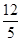，也就是说点T在平移后的直线AB上（即平移后的直线AB与x轴的交点），易求得直线AB的斜率，结合点T的坐标，即可得到平移后直线AB的解析式，联立抛物线的解析式可求得M点的横坐标．