
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),已知
左侧),已知![]() 点的纵坐标是2.
点的纵坐标是2.
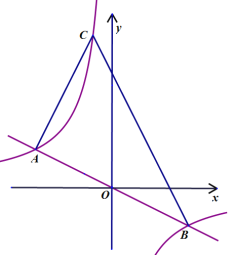
(1)求反比例函数的表达式;
(2)点![]() 上方的双曲线上有一点
上方的双曲线上有一点![]() ,如果
,如果![]() 的面积为30,直线
的面积为30,直线![]() 的函数表达式.
的函数表达式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)直线l1:![]() 经过点A,且A点的纵坐标是2,可得A(-4,2),代入反比例函数解析式可得k的值;
经过点A,且A点的纵坐标是2,可得A(-4,2),代入反比例函数解析式可得k的值;
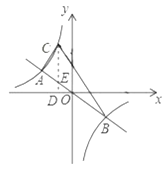
(2)根据中心对称求得B的坐标,过C作CD⊥x轴于D,交AB于E,求得E点的坐标,进而求得CE,然后根据两个三角形面积的和等于△ABC的面积,列出方程,解方程求得C的坐标,然后根据待定系数法求得即可.
解:(1)直线![]() 经过点
经过点![]() ,且
,且![]() 点的纵坐标是2,
点的纵坐标是2,
∴令![]() ,则
,则![]() ,即
,即![]() ,
,
∵反比例函数![]() 的图象经过
的图象经过![]() 点,
点,
∴![]() ,
,
∴反比例函数的表达式为![]() ;
;
(2)作![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,
,
∴直线![]() 和双曲线
和双曲线![]() 是中心对称图象,
是中心对称图象,![]() ,
,
∴![]() ,
,
设![]() ,把
,把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
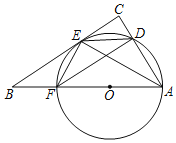
【题目】如图,AF为⊙O的直径,点B在AF的延长线上,BE切⊙O于点E,过点A作AC⊥BE,交BE的延长线交于点C,交⊙O交于点D,连接AE,EF,FD,DE.
(1)求证:EF=ED.
(2)求证:DFAF=2AEEF.
(3)若AE=4![]() ,DE=2
,DE=2![]() ,求sin∠DFA的值.
,求sin∠DFA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
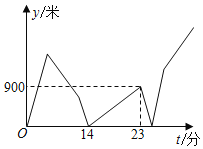
【题目】已知A、B、C三地顺次在同一直线上,甲、乙两人均骑车从A地出发,向C地匀速行驶.甲比乙早出发5分钟,甲到达B地并休息了2分钟后,乙追上了甲.甲、乙同时从B地以各自原速继续向C地行驶.当乙到达C地后,乙立即掉头并提速为原速的![]() 倍按原路返回A地,而甲也立即提速为原速的
倍按原路返回A地,而甲也立即提速为原速的![]() 倍继续向C地行驶,到达C地就停止.若甲、乙间的距离y(米)与甲出发的时间t(分)之间的函数关系如图所示,则当甲到达C地时,乙距A地_____米.
倍继续向C地行驶,到达C地就停止.若甲、乙间的距离y(米)与甲出发的时间t(分)之间的函数关系如图所示,则当甲到达C地时,乙距A地_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题.
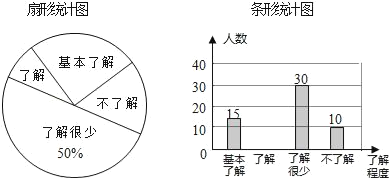
(1)接受问卷调查的学生共有 名,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;请补全条形统计图;
(2)若该校共有学生1200人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解””和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在二次函数y=ax2+bx+c(a≠0)的图象中,小明同学观察得出了下面几条信息:①b2﹣4ac>0;②abc<0;③![]() ;④b2=4a(c﹣1);⑤关于x的一元二次方程ax2+bx+c=3无实数根,共中信息错误的个数为( )
;④b2=4a(c﹣1);⑤关于x的一元二次方程ax2+bx+c=3无实数根,共中信息错误的个数为( )
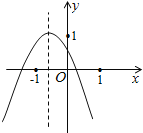
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从有400人的某小区抽取40名人员的答卷成绩,并对他们的成绩(单位:分)统计如下:
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
80 | 60 | 80 | 95 | 85 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
根据数据绘制了如下的表格和统计图:
等级 | 成绩( | 频率 | 频率 |
|
| 10 | 0.25 |
|
|
| |
|
| 12 | 0.3 |
|
|
| |
合计 | 40 | 1 | |
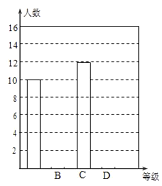
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
(4)该社区有2名男管理员和2名女管理员,现从中随机挑选2名管理员参加“社区防控”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
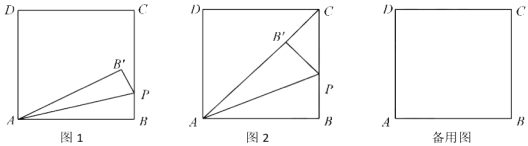
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点
轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
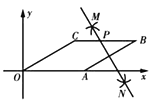
A.![]() B.
B.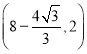 C.
C.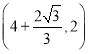 D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com