
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DBEC.(填“>”,“<”或“=”)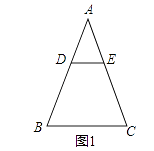
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.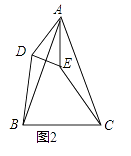
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.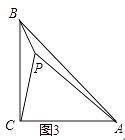
【答案】
(1)=
(2)
解:成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中
得 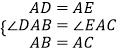
∴△DAB≌△EAC,
∴DB=CE
(3)
解:如图,
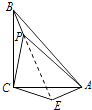
将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2 ![]() ,
,
在△PEA中,PE2=(2 ![]() )2=8,AE2=12=1,PA2=32=9,
)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA
∴∠BPC=∠CEA=135°
【解析】解:(1)∵DE∥BC,
∴ ![]() ,
,
∵AB=AC,
∴DB=EC,
故答案为:=,
(1)由DE∥BC,得到 ![]() ,结合AB=AC,得到DB=EC;(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
,结合AB=AC,得到DB=EC;(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y= ![]() x2(0≤x≤2)的图象记为曲线C1 , 将C1绕坐标原点O逆时针旋转90°,得曲线C2 .
x2(0≤x≤2)的图象记为曲线C1 , 将C1绕坐标原点O逆时针旋转90°,得曲线C2 . 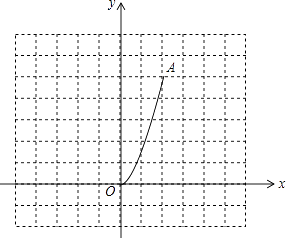
(1)请画出C2;
(2)写出旋转后A(2,5)的对应点A1的坐标;
(3)直接写出C1旋转至C2过程中扫过的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )

A. AC=AC B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用直尺和圆规作一个角等于已知角的作法如下:
①以点O为圆心,以任意长为半径画弧,分别交OA、OB于点D、C;
②作射线O′B′,以点O′为圆心,以 长为半径画弧,交O′B′于点C′;
③以点C′为圆心,以 长为半径画弧,两弧交于点D′;
④过点D′作射线O′A′,∴∠A′O′B′为所求.
(1)请将上面的作法补充完整;
(2)△OCD≌△O′C′D′的依据是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和![]() 个过滤网要花费
个过滤网要花费![]() 元,买
元,买![]() 个空气净化器和
个空气净化器和![]() 个过滤网要花费
个过滤网要花费![]() 元.
元.
(![]() )请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(![]() )为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买
)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买![]() 个空气净化器和
个空气净化器和![]() 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com