
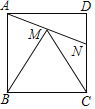
【题目】如图,在正方形![]() 内,以
内,以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() 并延长交
并延长交![]() 于
于![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据四边形ABCD是正方形,△EMC是等边三角形,得出∠BAM=∠BMA=∠CMD=∠CDM=(180°-30°)=75°,再计算角度即可;通过做辅助线MD,得出MA=MD,MD=MN,从而得出AM=MN.
如图,连接DM,
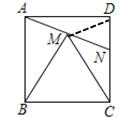
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠ADC=90°,
∵△EMC是等边三角形,
∴BM=BC=CM,∠EMC=∠MBC=∠MCB=60°,
∴∠ABM=∠MCN=30°,
∵ BA=BM, MC=CD,
∴∠BAM=∠BMA=∠CMD=∠CDM=(180°-30°)=75°,
∴∠MAD=∠MDA=15°, 故A正确;
∴MA=MD,
∴∠DMN=∠MAD+∠ADM=30°,
∴∠CMN=∠CMD-∠DMN=45°,故B正确;
∵∠MDN=∠AND=75°
∴MD=MN
∴AM=MN,故C正确;
∵∠CMN=45°,∠MCN=30°,
∴![]() ,故D错误,故选D.
,故D错误,故选D.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x+3.
(1)在网格中,画出该函数的图象.
(2)(1)中图象与![]() 轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中, ∠ACB=90°,∠CAB=30°,以AC,AB为边向外作等边三角形ACD和等边三角形ABE,点F在AB上,且到AE,BE的距离相等.
(1)用尺规作出点F; (要求:尺规作图,保留作图痕迹,不写作法)
(2)连接EF,DF,证明四边形ADFE为平行四边形.
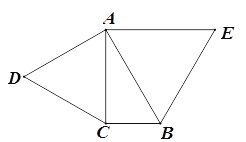
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,点
中,点![]() 为
为![]() 边中点,点
边中点,点![]() 为
为![]() 边中点;点
边中点;点![]() ,
, ![]() 为
为![]() 边三等分点,
边三等分点, ![]() ,
, ![]() 为
为![]() 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形
边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形![]() 的面积与图3中四边形
的面积与图3中四边形![]() 的面积相等吗?
的面积相等吗?
(1)小瑞的探究过程如下
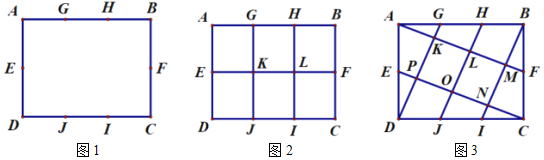
在图2中,小瑞发现, ![]() ;
;
在图3中,小瑞对四边形![]() 面积的探究如下. 请你将小瑞的思路填写完整:
面积的探究如下. 请你将小瑞的思路填写完整:
设![]() ,
, ![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
∵![]()
∴![]() ,且相似比为
,且相似比为![]() ,得到
,得到![]()
又∵![]() ,
, ![]()
∴![]()
∴![]() ,
, ![]() ,
, ![]()
∴![]() ,则
,则![]() (填写“
(填写“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
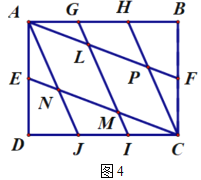
(2)小瑞又按照图4的方式连接矩形![]() 对边上的点.则
对边上的点.则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
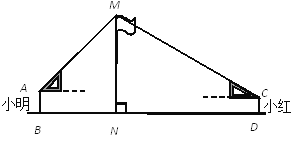
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,结果保留整数.)
,结果保留整数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
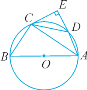
【题目】如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,连接CD且DC=BC,过C点作AD的垂线交AD延长线于E.
(1)求证:CE是⊙O的切线;
(2)若AB=5,AC=4,求tan∠DCE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
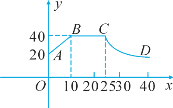
【题目】心理学家研究发现,一般情况下,在一节40分钟的课中,学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数解析式,并写出自变量的取值范围;
(2)开始上课后第5分钟时与第30分钟时比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数至少为36,那么经过适当安排,老师能否在学生达到所需的状态下讲解完这道题目?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的顶点
的顶点![]() 在坐标原点,正方形
在坐标原点,正方形![]() 的边
的边![]() 与
与![]() 在同一直线上,
在同一直线上, ![]() 与
与![]() 在同一直线上,且
在同一直线上,且![]() ,
,![]() 边和
边和![]() 边所在直线的解析式分别为:
边所在直线的解析式分别为: ![]() 和
和![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
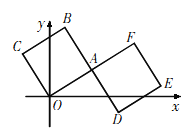
A.(6,-1)B.(7,-1)C.(7,-2)D.(6,-2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com