
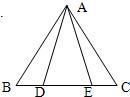
 22、如图,已知D、E是等腰△ABC底边BC上两点,且BD=CE.求证:∠ADE=∠AED.
22、如图,已知D、E是等腰△ABC底边BC上两点,且BD=CE.求证:∠ADE=∠AED.

科目:初中数学 来源: 题型:
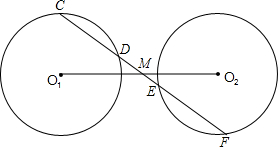 助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)
助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)查看答案和解析>>
科目:初中数学 来源:第3章《圆的基本性质》中考题集(13):3.4 圆周角(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2009年福建省南平市初中学业质量检查数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com