
【题目】如图,四边形![]() 中,
中,![]() 平分
平分![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
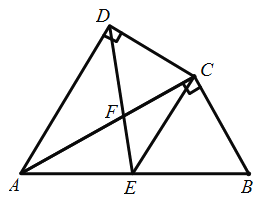
(1)由∠DAC=∠CAB,∠ADC=∠ACB=90°,可得;(2)根据直角三角形斜边上中线性质得∠EAC=∠ECA,证∠DAC=∠ECA,可得;(3)证△AFD∽△CFE,根据相似三角形性质可得:AD:CE=AF:CF.
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ACD∽△ABC,
(2)证明:∵E为AB的中点,
∴CE=![]() AB=AE,
AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=![]() AB,
AB,
∴CE=![]() ×6=3,
×6=3,
∵AD=4,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
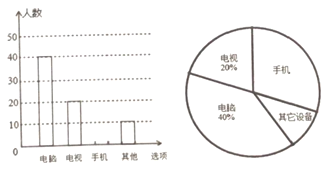
【题目】受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动.为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它”四种类型的设备对学生做了一次抽样调查.调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有1500名学生,估计全校用手机上网课的学生共有___________名;
(3)在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D. 对称轴为直线x=1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了疫情防控需要,某防护用品厂计划生产150000个口罩,但是在实际生产时,……,求实际每天生产口罩的个数,在这个题目中,若设实际每天生产口罩x个,可得方程![]() =10,则题目中用“……”表示的条件应是( )
=10,则题目中用“……”表示的条件应是( )
A.每天比原计划多生产500个,结果延期10天完成
B.每天比原计划少生产500个,结果提前10天完成
C.每天比原计划少生产500个,结果延期10天完成
D.每天比原计划多生产500个,结果提前10天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.

(1)l经过点B,求它的解析式,并写出此时l的对称轴及顶点坐标:
(2)设点C的纵坐标为yc,求yc的最大值,此时l上有两点(x1,y1),(x2,y2),其中x1>x2≥0,比较y1与y1的大小;
(3)当线段OA被l只分为两部分,且这两部分的比是1:4时,求h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
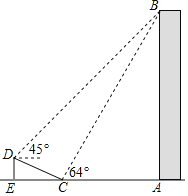
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,可得到△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1,则△AnCnCn+1的周长为_______(n≥1,且n为整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
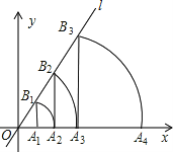
【题目】在直角坐标系中,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3…按照这样的作法进行下去,则点A20的坐标是______.
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3…按照这样的作法进行下去,则点A20的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
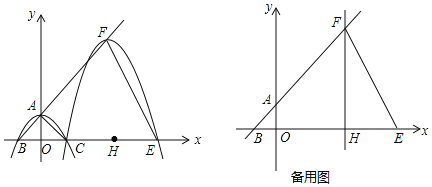
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B、C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
(1)求a、c的值;
(2)连接OF,求△OEF的周长;
(3)现将一足够大的三角板的直角顶点Q放在射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P,是否存在这样的点Q,使得以点P、Q、E为顶点的三角形与△POE全等?若存在,请直接写出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com