
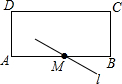
 如图所示,在矩形ABCD中,AD=4cm,AB=10cm,点M是AB边上的中点,将点A沿着过点M的直线l翻折使点A落在DC边上,点A的对称点为点P,则PD=2cm或8cm.
如图所示,在矩形ABCD中,AD=4cm,AB=10cm,点M是AB边上的中点,将点A沿着过点M的直线l翻折使点A落在DC边上,点A的对称点为点P,则PD=2cm或8cm. 分析 由矩形的性质得出CD=AB=10cm,求出AM=BM=5cm,分两种情况:
①当直线l与AD相交时,作MN⊥CD于N,则MN=AD=4cm,PM=AM=5cm,DN=AM=5cm,由勾股定理求出PN,即可得出结果;
②当直线l与CD相交时,作MF⊥CD于F,则MF=AD=4cm,PM=AM=5cm,由勾股定理求出PF,即可得出结果.
解答 解: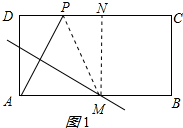 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴CD=AB=10cm,
∵点M是AB边上的中点,
∴AM=BM=5cm,
分两种情况:
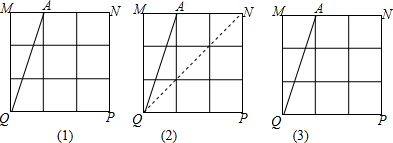
①当直线l与AD相交时,如图1所示:
作MN⊥CD于N,则MN=AD=4cm,PM=AM=5cm,DN=AM=5cm,
∴PN=$\sqrt{P{M}^{2}-M{N}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3(cm),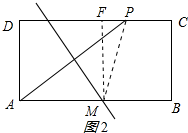
∴PD=DN-PN=2cm;
②当直线l与CD相交时,如图2所示:
作MF⊥CD于F,则MF=AD=4cm,PM=AM=5cm,
∴PF=$\sqrt{P{M}^{2}-M{F}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3(cm),
∴PD=DF+PF=8cm;
综上所述:PD的长为2cm或8cm;
故答案为:2cm或8cm.
点评 本题考查了矩形的性质、勾股定理、折叠的性质;熟练掌握矩形和折叠的性质,由勾股定理求出PN和PF是解决问题的关键.


科目:初中数学 来源: 题型:解答题
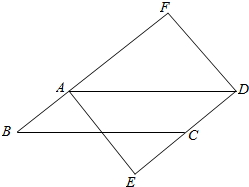 如图,在?ABCD中,过点A作AE⊥DC交DC的延长线于点E过点D作DF⊥BA,交BA的延长线于点F.
如图,在?ABCD中,过点A作AE⊥DC交DC的延长线于点E过点D作DF⊥BA,交BA的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播无棣新闻 | |
| B. | 今年春节,我们县的天气一定是晴天 | |
| C. | “大衣哥”朱之文一定能上2016年春节联欢晚会 | |
| D. | 从一个只装有红球的箱子里摸出一个球,摸出的球是红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -7,2 | B. | -$\frac{1}{7}$,2 | C. | -$\frac{1}{7}$,3 | D. | $\frac{1}{7}$,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com