
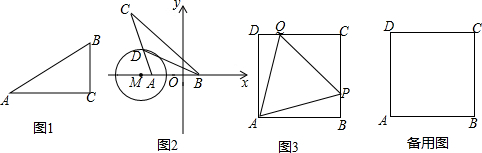
分析 (1)先画一条线段AB,再确定AB的中点O,以点O为圆心,AB为半径画圆,在圆O上取一点C,连接AC、BC,则△ABC是所求作的三角形;
(2)设AC=2x=BD,则AD=CD=x,从而表示出BC=$\sqrt{3}$x,利用勾股定理得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{7}$x,从而求得三条线段的比;
(3)利用两边对应成比例且夹角相等证得△AMD∽△DMB后得到BD=2AD=AC,从而说明三角形ABC是好玩三角形;
(4)当点P在AB上时,△APQ是等腰直角三角形,不可能是“好玩三角形”,然后分等腰三角形APQ底边PQ等于AE,即PQ=AE时和等腰三角形APQ的腰AP与它的中线QM相等两种情况求得结论即可.
解答 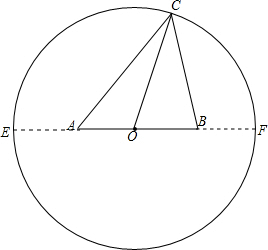 解:(1)如图,①作一条线段AB,
解:(1)如图,①作一条线段AB,
②作线段AB的中点O,
③以点O为圆心,AB为半径画圆,
④在圆O上取一点C,连接AC、BC,
∴△ABC是所求作的三角形(点E、F除外).
(2)如图1,由题意可得,只能是AC边上的中线BD等于AC,
设AC=2x=BD,则AD=CD=x,
所以,BC=$\sqrt{3}$x,则AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{7}$x,
所以,BC:AC:AB=$\sqrt{3}$:2:$\sqrt{7}$;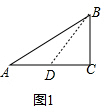
(3)如图2,三角形AMD中,
AM=2,MD=4,
三角形MBD中,MD=4,MB=8,
又∵∠DMA=∠BMD,
∴△AMD∽△DMB,
∴BD=2AD=AC,
∴三角形ABC是好玩三角形;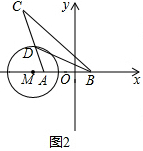
(4)当点P在AB上时,△APQ是等腰直角三角形,不可能是“好玩三角形”
当P在BC上时,连接AC交PQ于点E,
则△PCQ、△PCE、△QCE都是等腰直角三角形,
①如图3若等腰三角形APQ底边PQ等于AE,即PQ=AE时,
设PE=QE=x,
则AE=2x,
∴AC=AE+CE=3x,
a=$\frac{3x}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$x,s=AB+BP=a+a-PC=2×$\frac{3\sqrt{2}}{2}$x-$\sqrt{2}$x=2$\sqrt{2}$x,
∴$\frac{a}{s}$=$\frac{3}{4}$;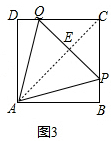
②如图4,若等腰三角形APQ的腰AP与它的中线QM相等,
即AP=QM时,可得QM=AP=AQ,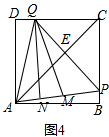
作QN⊥AP于N,∴MN=AN=$\frac{1}{2}$PM,
设MN=x,则QN=$\sqrt{A{Q}^{2}-A{N}^{2}}$=$\sqrt{15}$x,
tan∠APQ=$\frac{QN}{PN}$=$\frac{\sqrt{15}}{3}$,同时tan∠APQ=$\frac{AE}{PE}$,
∴$\frac{AE}{PE}$=$\frac{\sqrt{15}}{3}$,
∴AE=$\sqrt{15}$k,PE=CE=3k,
∴AC=AE+CE=($\sqrt{15}$+3)k,
∴a=$\frac{AC}{\sqrt{2}}$=$\frac{\sqrt{15}+3}{\sqrt{2}}$k,
∴PC=$\sqrt{2}$PE,
∴PB=a-PC=$\frac{\sqrt{15}+3}{\sqrt{2}}$k-3$\sqrt{2}$k=$\frac{\sqrt{30}-3\sqrt{2}}{2}$k,
∴s=a+PB=$\frac{\sqrt{30}+3\sqrt{2}}{2}$k+$\frac{\sqrt{30}-3\sqrt{2}}{2}$k=$\sqrt{30}$k,
∴$\frac{a}{s}$=$\frac{\sqrt{15}+3}{\sqrt{2}}$×$\frac{1}{\sqrt{30}}$=$\frac{5+\sqrt{15}}{10}$.
点评 本题是一道相似形综合运用的试题,考查了相似三角形的判定及性质的运用,勾股定理的运用,等腰直角三角形的性质的运用,等腰三角形的性质的运用,锐角三角形函数值的运用,解答时灵活运用三角函数值建立方程求解是解答的关键.


科目:初中数学 来源: 题型:选择题
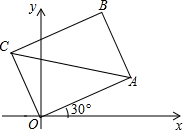 如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )
如图,矩形OABC的一顶点O恰好落在平面直角坐标系的坐标原点处,边OA与x轴正方向的夹角为30°.连结AC.若AB=6,AC=10,则点A的坐标为( )| A. | ($4\sqrt{3}$,4) | B. | (4,4) | C. | (4,$4\sqrt{3}$) | D. | (4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
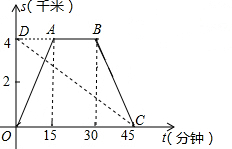 玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
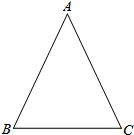 如图,在△ABC中,AB=AC=4$\sqrt{5}$,sinC=$\frac{2\sqrt{5}}{5}$
如图,在△ABC中,AB=AC=4$\sqrt{5}$,sinC=$\frac{2\sqrt{5}}{5}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 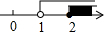 | B. | 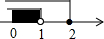 | C. | 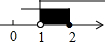 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+7>b+7 | B. | 2a>2b | C. | -5a>-5b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com