练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．解分式方程：$\frac{1}{x-3}$+$\frac{x-4}{x+3}$=1．

    分析 方程两边同时乘以（x-3）（x+3），然后求出方程的解，最后验根．

    解答 解：方程两边同乘以（x+3）（x-3），
    得x+3+（x-4）（x-3）=（x+3）（x-3），
    整理得-6x=-24，
    系数化为1，得x=4，
    经检验，x=4是原分式方程的解．

    点评 本题主要考查了解分式方程的知识，解答本题的关键是掌握解分式方程的步骤，注意要验根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．解方程
    （1）（x-2）3=-0.125
    （2）x2-$\frac{25}{16}$=0
    （3）（2x+3）（x-4）-（x+2）（x-3）=6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．一家文具超市营业员的流水账记录；五月一日卖出15本笔记本和5只计算器，收入225元，五月二日以同样的价格卖出同样的3本笔记本和6只计算器，收入285元，请你用二元一次方程组的知识进行分析，这个记录是否有错误？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解分式方程：$\frac{x-5}{x}$+$\frac{x+1}{2x}$=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，点O是正方形ABCD两条对角线的交点，分别延长CO到点G，OC到点E，使OG=2OD、OE=2OC，然后以OG、OE为邻边作正方形OEFG．
    （1）如图1，若正方形OEFG的对角线交点为M，求证：四边形CDME是平行四边形．
    （2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转，得到正方形OE′F′G′，如图2，连接AG′，DE′，求证：AG′=DE′，AG′⊥DE′；
    （3）在（2）的条件下，正方形OE′F′G′的边OG′与正方形ABCD的边相交于点N，如图3，设旋转角为α（0°＜α＜180°），若△AON是等腰三角形，请直接写出α的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．2015年12月9日德国《柏林日报》报道，全球各地销售的近四分之三的玩具都是由中国工厂生产的，若中国某玩具工厂生产了一批玩具共3000个，为检测该批玩具的质量是否合格，质检人员从中随机抽查了300个，合格的有290个，在此次调查中，所抽取的300个玩具的合格情况是（　　）
    A．总体B．个体C．样本D．样本容量

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

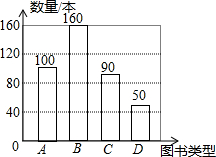    16．王洋同学调查了光明中学图书馆中某周A，B，C，D四类图书的借阅人数（每人每次只能借阅一本图书），并绘制成了如图所示的条形统计图，若根据该条形统计图绘制扇形统计图，则B类图书借阅人数所在的扇形的圆心角的度数为144°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

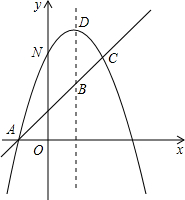    13．如图，已知抛物线y=-x2+bx+c与一直线相交于A（-1，0），C（2，3）两点，与y轴交于点N．其顶点为D．
    （1）抛物线及直线AC的函数关系式；
    （2）点M在直线x=3上，求使MN+MD的值最小时的M点坐标；
    （3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．解方程组：
    （1）$\left\{\begin{array}{l}{y=2x-3}\\{3x+2y=8}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{x+y=7}\\{3x+y=17}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案