
分析 (1)首先提取公因式2y,进而利用完全平方公式分解因式即可;
(2)首先提取公因式(x-y),进而利用平方差公式分解因式得出即可;
(3)直接利用平方差公式分解因式得出即可;
(4)直接利用完全平方公式分解因式进而利用平方差公式分解因式.
解答 解:(1)2x2y-8xy+8y=2y(x2-4x+4)=2y(x-2)2;
(2)a2(x-y)-9b2(x-y)
=(x-y)(a2-9b2)
=(x-y)(a+3b)(a-3b);
(3)9(3m+2n)2-4(m-2n)2
=[3(3m+2n)-2(m-2n)][3(3m+2n)+2(m-2n)]
=(7m+10n)(11m+2n);
(4)(y2-1)2+6(1-y2)+9
=(y2-1-3)2
=(y+2)2(y-2)2.
点评 此题主要考查了提取公因式法以及公式法分解因式,熟练应用乘法公式是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
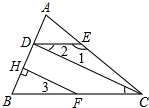 完成证明并写出推理根据:
完成证明并写出推理根据:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
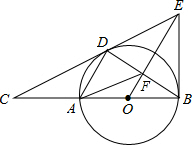 如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF.
如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.
某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的四边形是矩形 | B. | 对角线互相垂直的四边形是正方形 | ||
| C. | 平行四边形的对角线平分一组对角 | D. | 矩形的对角线相等且互相平分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com