
| �����n | 100 | 200 | 1500 | 2000 | 2500 |
| һ��Ʒ��m | 94 | 194 | 1430 | 1902 | 2375 |
| һ��ƷƵ��$\frac{m}{n}$ | 0.94 | 0.97 | 0.95 | 0.95 | 0.95 |
���� ��1������Ƶ��=Ƶ��������������Ƶ��=����������Ƶ�ʼ�����⣻
��2�������ظ�ʵ��ʱ���¼�������Ƶ�ʿɿ���������¼��ĸ��ʣ����ݱ��ɵ������ȡ1�����������1��Ʒ�ĸ���ԼΪ0.95��
��3��������������=Ƶ����Ƶ����ʽ�����㼴�ɣ�
��� �⣺��1��������£�
| �����n | 100 | 200 | 1500 | 2000 | 2500 |
| һ��Ʒ��m | 94 | 194 | 1430 | 1902 | 2375 |
| һ��ƷƵ��m/n | 0.94 | 0.97 | 0.95 | 0.95 | 0.95 |
���� ���⿼��������Ƶ�ʹ��Ƹ��ʣ���������������Ƶ���ȶ�ֵ�����ʣ��õ���֪ʶ��Ϊ��Ƶ��=Ƶ��������������Ƶ��=����������Ƶ�ʣ���������=Ƶ����Ƶ�ʣ�Ƶ��=������������������֮�ȣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
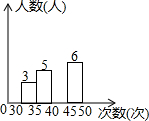 Ϊ�˽�ijУ���꼶Ů��1�������������Ĵ������������������50��Ů���μ�1�������������Ĵ������ԣ������Ƴ�һ����������Ƶ���ֲ�ֱ��ͼ����ͼ������1�������������Ĵ�����40-45��Ƶ����0.72��
Ϊ�˽�ijУ���꼶Ů��1�������������Ĵ������������������50��Ů���μ�1�������������Ĵ������ԣ������Ƴ�һ����������Ƶ���ֲ�ֱ��ͼ����ͼ������1�������������Ĵ�����40-45��Ƶ����0.72���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x2+3x2=5x4 | B�� | -5x2+��3x��2=4x2 | C�� | 2x2•3x3=6x6 | D�� | 2x2•x3=4x5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ijС���ڡ���Ƶ�ʹ��Ƹ��ʡ��������У�ͳ����ij�ֽ�����ֵ�Ƶ�ʣ���������ͼ��ʾ������ͼ����ô������һ������������п��ܵ��ǣ�������
ijС���ڡ���Ƶ�ʹ��Ƹ��ʡ��������У�ͳ����ij�ֽ�����ֵ�Ƶ�ʣ���������ͼ��ʾ������ͼ����ô������һ������������п��ܵ��ǣ�������| A�� | ��װ��1�������2��������ɫ����ȫ��ͬ���IJ����������������һ�����ǡ����� | |
| B�� | ��һ���˿����������ȡһ�ţ��������ǡ���ɫ�ġ� | |
| C�� | ��һö�ʵؾ��ȵ�Ӳ�ң����ʱ����ǡ����泯�ϡ� | |
| D�� | ֻһ���ʵؾ��ȵ������������ӣ����ʱ�泯�ϵĵ�����6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪���κ���y=a��x+l����x-3����x�ύ��A��B���㣨��A��
��֪���κ���y=a��x+l����x-3����x�ύ��A��B���㣨��A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ӻ����ڲ���ŷ�ޱ� | |
| B�� | ���ڵ���������� | |
| C�� | ��һö�ʵؾ��ȵ����ӣ������ĵ���Ϊ8 | |
| D�� | ƽ����ͬһ��ֱ�ߵ�����ֱ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16 | B�� | 18 | C�� | 20 | D�� | 25 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com