
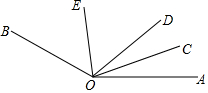
 如图所示,OC、OE分别是∠AOD、∠BOD的平分线,且∠AOB=150°,求∠COE的度数.
如图所示,OC、OE分别是∠AOD、∠BOD的平分线,且∠AOB=150°,求∠COE的度数. 分析 由角平分线的定义可求得∠DOE=$\frac{1}{2}$∠BOD,∠COD=$\frac{1}{2}$∠AOD,再利用角的和差可求得答案.
解答 解:
∵OC、OE分别是∠AOD、∠BOD的平分线,
∴∠DOE=$\frac{1}{2}$∠BOD,∠COD=$\frac{1}{2}$∠AOD,
∴∠COE=∠DOE+∠COD=$\frac{1}{2}$∠BOD+$\frac{1}{2}$∠AOD=$\frac{1}{2}$(∠BOD+∠AOD)=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×150°=75°.
点评 本题主要考查角平分线的定义,掌握角平分线把角分成两个相等的角是解题的关键.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | [x-(2y+1)]2 | B. | [x+(2y+1)]2 | C. | [x-(2y-1)][x+(2y-1)] | D. | [(x-2y)+1][(x-2y)-1] |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
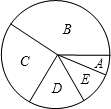 某校团委在寒假期间组织了以“合理安排时间,养成阅读习惯”为主题的教育活动,在学校随机调查了50名同学平均每天的阅读时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题:
某校团委在寒假期间组织了以“合理安排时间,养成阅读习惯”为主题的教育活动,在学校随机调查了50名同学平均每天的阅读时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题:| 组别 | 阅读的时间 | 频数 | 频率 |
| A | 1≤t<2 | 3 | 0.06 |
| B | 2≤t<4 | 20 | 0.40 |
| C | 4≤t<6 | m | 0.30 |
| D | 6≤t<8 | 8 | n |
| E | t≥8 | 4 | 0.08 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com