
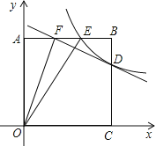
����Ŀ����ͼ��������AOCB�ı߳�Ϊ4��������������ͼ�����E��3��4����
��1�����������Ľ���ʽ��
��2��������������ͼ�����߶�BC���ڵ�D��ֱ��![]() ����D�����߶�AB�ཻ�ڵ�F�����F�����ꣻ
����D�����߶�AB�ཻ�ڵ�F�����F�����ꣻ
��3������OF��OE��̽����AOF���EOC��������ϵ����֤����
��4������P��x���ϵĶ��㣬��Q�ǣ�1���еķ����������ڵ�һ����ͼ���ϵĶ��㣬��ʹ����PDQΪ����ֱ�������Σ��������P�����꣮
���𰸡���1��y��![]() ����2����F������Ϊ��2��4������3����AOF��
����2����F������Ϊ��2��4������3����AOF��![]() ��EOC�����ɼ���������4��P�������ǣ�
��EOC�����ɼ���������4��P�������ǣ�![]() ��0����-5��0����
��0����-5��0����![]() ��0����5��0��
��0����5��0��
��������
��1���跴���������Ľ���ʽΪy��![]() ���ѵ�E��3��4�����뼴�����k��ֵ�������ó����ۣ�
���ѵ�E��3��4�����뼴�����k��ֵ�������ó����ۣ�
��2����������AOCB�ı߳�Ϊ4���ʿ�֪��D�ĺ�����Ϊ4����F��������Ϊ4�����ڵ�D�ڷ�����������ͼ���ϣ����Ե�D��������Ϊ3����D��4��3�����ɵ�D��ֱ��![]() �Ͽɵó�b��ֵ�������ó���ֱ�ߵĽ���ʽ���ٰ�y=4����ֱ�ߵĽ���ʽ���������F�����ꣻ
�Ͽɵó�b��ֵ�������ó���ֱ�ߵĽ���ʽ���ٰ�y=4����ֱ�ߵĽ���ʽ���������F�����ꣻ
��3����CD��ȡCG=AF=2������OG������EG���ӳ���x���ڵ�H����ȫ�������ε��ж�������֪��OAF�ա�OCG����EGB�ա�HGC��ASA�����ʿɵó�EG=HG����ֱ��EG�Ľ���ʽΪy=mx+n����E��3��4����G��4��2�����뼴�����ֱ��EG�Ľ���ʽ���ʿɵó�H������꣬��Rt��AOF�У�AO=4��AE=3�����ݹ��ɶ�����OE=5����֪OC=OE����OG�ǵ��������εױ�EF�ϵ����ߣ�����OG�ǵ��������ζ��ǵ�ƽ���ߣ��ɴ˼��ɵó����ۣ�
��4���֡�PDQ�������Ƿֱ���ֱ�ǣ���������������ۣ���DK��x�ᣬ��QR��x�ᣬ��DL��QR���ڵ�L�����ɹ���ȫ�ȵ�ֱ�������Σ����P�����꣬���ݵ���ͼ���ϣ���һ�����㺯���Ľ���ʽ������⣬
�⣺
��1���跴���������Ľ���ʽy��![]() ��
��
�߷�����������ͼ�����E��3��4����
��4��![]() ����k��12��
����k��12��
�෴���������Ľ���ʽy��![]() ��
��
��2����������AOCB�ı߳�Ϊ4��
���D�ĺ�����Ϊ4����F��������Ϊ4��
�ߵ�D�ڷ�����������ͼ���ϣ�
���D��������Ϊ3����D��4��3����
�ߵ�D��ֱ��y����![]() x+b�ϣ�
x+b�ϣ�
��3����![]() ��4+b��
��4+b��
��ã�b��5��
��ֱ��DFΪy����![]() x+5��
x+5��
��y��4����y����![]() x+5��
x+5��
��4����![]() x+5��
x+5��
��ã�x��2��
���F��������2��4����
��3����AOF��![]() ��EOC��������
��EOC��������
֤������CD��ȡCG��AF��2������OG������EG���ӳ���x���ڵ�H��

![]()
 ��
��
���OAF�ա�OCG��SAS����
���AOF����COG��
![]()
 ��
��
���EGB�ա�HGC��ASA����
��EG��HG��
��ֱ��EG��y��mx+n��
��E��3��4����G��4��2����
��![]() ��
��
���![]() ��
��
��ֱ��EG��y����2x+10��
��y����2x+10��0����x��5��
��H��5��0����OH��5��
��Rt��AOE�У�AO��4��AE��3�����ݹ��ɶ�����OE��5��
��OH��OE��
��OG�ǵ��������εױ�EH�ϵ����ߣ�
��OG�ǵ��������ζ��ǵ�ƽ���ߣ�
���EOG����GOH��
���EOG����GOC����AOF��
����AOF��![]() ��EOC��
��EOC��
��4����Q��D���Ҳࣨ��ͼ1�����ҡ�PDQ=90��ʱ����DK��x�ᣬ��QL��DK���ڵ�L��

����DPK�ա�QDK��
��P�������ǣ�a��0������KP=DL=4-a��QL=DK=3����Q�������ǣ�4+3��4-3+a������7��-1+a����
�ѣ�7��-1+a������y=![]() �ã�
�ã�
7��-1+a��=12��
��ã�a=![]() ��
��
��P�������ǣ�![]() ��0����
��0����
��Q��D����ࣨ��ͼ2�����ҡ�PDQ=90��ʱ����DK��x�ᣬ��QR��x�ᣬ��DL��QR���ڵ�L��

����QDL�ա�PDK��
��DK=DL=3����P��������b����PK=QL=4-b����QR=4-b+3=7-b��OR=OK-DL=4-3=1��
��Q�������ǣ�1��7-b��������y=![]() �ã�
�ã�
b=-5��
��P�������ǣ�-5��0����
��Q��D���Ҳࣨ��ͼ3�����ҡ�DQP=90��ʱ����DK��x�ᣬ��QR��x�ᣬ��DL��QR���ڵ�L��

����QDL�ա�PQK����DK=DL=3��
��Q�������c������������![]() ��
��
��QK=QL=![]() ��
��
�֡�QL=c-4��
��c-4=![]() ��
��
��ã�c=-2����ȥ����6��
��PK=DL=DR-LR=DR-QK=3-![]() =1��
=1��
��OP=OK-PK=6-1=5��
��P�������ǣ�5��0����
��Q��D����ࣨ��ͼ3�����ҡ�DQP=90��ʱ����������
����DPQ=90��ʱ������ͼ4������DK��x�ᣬ��QR��x�ᣬ
����DPR�ա�PQK��

��DR=PK=3��RP=QK��
��P�������ǣ�d��0����
��RK=QK=d-4��
��OK=OP+PK=d+3��
��Q�������ǣ�d+3��d-4��������y=![]() �ã�
�ã�
��d+3����d-4��=12��
��ã�d=![]() ��
��![]() ����ȥ����
����ȥ����
��P�������ǣ�![]() ��0����
��0����
����������P�������ǣ�![]() ��0����-5��0����
��0����-5��0����![]() ��0����5��0����
��0����5��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ݮ��ժ����ݮƷ����ͬ�����ۼ۸���ÿǧ��30Ԫ�����Ҿ��Ƴ�������ĩ���Żݷ������ײ�ժ���Żݷ����ǣ��οͽ��蹺��60Ԫ����Ʊ����ժ����ݮ�����Żݣ��Ҳ�ժ���Żݷ����ǣ��οͽ�����Ҫ������Ʊ����ժ����ݮ����10ǧ�˺������������Żݣ��Ż��ڼ䣬��ij�ο͵���ݮ��ժ��Ϊ![]() ǧ�ˣ��ڼײ�ժ�����ܷ���Ϊ
ǧ�ˣ��ڼײ�ժ�����ܷ���Ϊ![]() Ԫ�����Ҳ�ժ�����ܷ���Ϊ
Ԫ�����Ҳ�ժ�����ܷ���Ϊ![]() Ԫ��
Ԫ��
��1����![]() ��
��![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2�����ο����ѡ���ժȥ��ժ�ȽϺ��㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ij��ͯװ��ÿ���ۼ�60Ԫ��ÿ���ڿ���300����Ϊ�˴���������������������ۣ��г����鷴ӳ��ÿ����1Ԫ��ÿ���ڿɶ���30������֪�ÿ�ͯװÿ���ɱ���40Ԫ����ÿ�ͯװÿ���ۼ�xԪ��ÿ���ڵ�������Ϊy����
��1����y��x֮��ĺ�����ϵʽ��
��2����ÿ���ۼ۶�Ϊ����Ԫʱ��ÿ���ڵ����������������������Ԫ��
��3����������ÿ������Ҫ��ò�����6480Ԫ������ÿ��������Ҫ���۸ÿ�ͯװ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
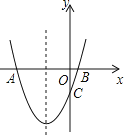
����Ŀ����ͼ��������y=x2+2x+k+1��x�ύ��A��B���㣬��y�ύ���C��0��-3����
��1���������ߵĶԳ��ἰk��ֵ��
��2���������ߵĶԳ����ϴ���һ��P��ʹ��PA+PC��ֵ��С�����ʱ��P�����ꣻ
��3����M���������ϵ�һ���㣬���ڵ������ޣ�
����M���˶����δ�ʱ����AMB�������������AMB������������ʱ��M�����꣮
����M���˶����δ�ʱ���ı���AMCB������������ı���AMCB������������ʱ��M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
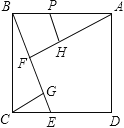
����Ŀ����ͼ����������ABCD�У���B��һֱ����CD�ཻ�ڵ�E����A��AF��ֱBE�ڵ�F����C��CG��ֱBE�ڵ�G����FA�Ͻ�ȡFH=FB���ٹ�H��HP��ֱAF��AB��P����CG=3������CGE���ı���BFHP�����֮��Ϊ��_________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD��ƽ���ı��Σ����н����д������(����)
�ٵ�AB��BCʱ���������Σ��ڵ�AC��BDʱ���������Σ��۵���ABC��90��ʱ�����Ǿ��Σ��ܵ�AC��BDʱ�����������Σ�
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
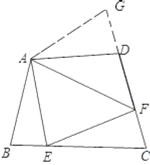
����Ŀ����ͼ�������ı���ABCD�У�AB=AD����B+��D=180����E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF=![]() ��BAD���ӳ�FD����G��ʹDG=BE������AG�����н��ۣ�����ABE�ա�ADG���ڡ�AEF�ա�AGF����EF=BE+DF����AD+BE��AF����ȷ����__________
��BAD���ӳ�FD����G��ʹDG=BE������AG�����н��ۣ�����ABE�ա�ADG���ڡ�AEF�ա�AGF����EF=BE+DF����AD+BE��AF����ȷ����__________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������й��Ŵ���ѧ����Ҫ��������������������߳ɾͣ����м��أ�����ţ�塢�����ֱ��ʮ����ţ�������壬ֱ��������ʣ�ţ�����ֱ�Σ����ģ��������� 5 ͷţ��2 ֻ��ֵ�� 10 ����2 ͷţ��5 ֻ��ֵ�� 8 �����ʣ�ÿͷţ��ÿֻ���ֵ����������� ��ÿͷţֵ�� x ����ÿֻ��ֵ�� y �������з����������ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڶ۽�������ABC����AB=6cm��AC=12cm������D��A�������B��ֹ������E��C�������A��ֹ.��D�˶����ٶ�Ϊ1cm/������E�˶����ٶ�Ϊ2cm��.�������ͬʱ�˶�����ô���Ե�A��D��EΪ��������������ABC����ʱ���˶���ʱ����( )
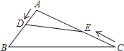
A. 3��2.8 B. 3��4.8 C. 1��4 D. 1��6
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com