
【题目】阅读下列材料:
小明遇到一个问题:已知:如图1,在△ABC中,∠BAC=120°,∠ABC=40°,试过△ABC的一个顶点画一条直线,将此三角形分割成两个等腰三角形.
他的做法是:如图2,首先保留最小角∠C,然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角,使∠DAC=20°,△ABC即可被分割成两个等腰三角形.
喜欢动脑筋的小明又继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
他的做法是:

如图3,先画△ADC ,使DA=DC,延长AD到点B,使△BCD也是等腰三角形,如果DC=BC,那么∠CDB =∠ABC,因为∠CDB=2∠A,所以∠ABC= 2∠A.于是小明得到了一个结论:
当三角形中有一个角是最小角的2倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
请你参考小明的做法继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请直接写出你所探究出的另外两条结论(不必写出探究过程或理由).
【答案】见解析。
【解析】
结论1:当三角形中的两个内角互余时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形. 结论2:当三角形中有一个角是另一个角的3倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
解:如图1,
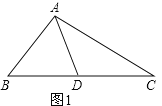
∠BAC=3∠C,作AD使∠CAD=∠C,
则∠BAD=∠BAC-∠CAD=2∠C,
又∠ADB=∠CAD+∠C=2∠C,
所以,△ACD与△ABD都是等腰三角形;
如图2,
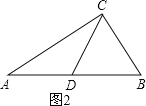
∠A+∠B=90°,
则∠ACB=180°-90°=90°,
作CD,使∠ACD=∠A,
则∠BCD=90°-∠ACD=90°-∠A=∠B,
即∠BCD=∠B,
所以,△ACD与△BCD都是等腰三角形.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的顶点坐标分别为A(﹣2,5),B(﹣4,3),C(﹣1,﹣1).

(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC关于y轴对称的△A2B2C2,并写出点A2的坐标;
(3)在边AC上有一点P(a、b),直接写出以上两次图形变换后的对称点P1、P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股点.
(1)已知点M、N是线段AB的勾股点,若AM=1,MN=2,求BN的长;
(2)如图2,点P(a,b)是反比例函数y=![]() (x>0)上的动点,直线y=﹣x+2与坐标轴分别交于A、B两点,过点P分别向x、y轴作垂线,垂足为C、D,且交线段AB于E、F.证明:E、F是线段AB的勾股点;
(x>0)上的动点,直线y=﹣x+2与坐标轴分别交于A、B两点,过点P分别向x、y轴作垂线,垂足为C、D,且交线段AB于E、F.证明:E、F是线段AB的勾股点;
(3)如图3,已知一次函数y=﹣x+3与坐标轴交于A、B两点,与二次函数y=x2﹣4x+m交于C、D两点,若C、D是线段AB的勾股点,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
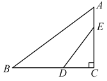
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2)
(1)连接A、B、C三点,请在如图中作出△ABC关于x轴对称的图形△A’B’C’并直接写出各对称点的坐标;(2)求△ABC的面积;(3)若M(x,y)是△ABC内部任意一点,请直接写出点M在△A’B’C’内部的对应点M1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年我市体育中考总分60分,其中男生1000米跑为必选项目,再在立定跳远、跳绳、实心球掷远、篮球运球和足球运球中选择两项;女生800米跑为必选项目,再在立定跳远、跳绳、仰卧起坐、篮球运球和足球运球中选择两项![]() 某校对得分超过40分的20位学生的成绩m进行统计,结果如频数分布表所示:
某校对得分超过40分的20位学生的成绩m进行统计,结果如频数分布表所示:

![]() 求a的值;
求a的值;
![]() 若用扇形图来描述,求分数在
若用扇形图来描述,求分数在![]() 内所对应的扇形图的圆心角的大小;
内所对应的扇形图的圆心角的大小;
![]() 若男生小明在刚开始训练时在选考项目随机选择两项进行训练,试用列举法求小明选择”跳绳
若男生小明在刚开始训练时在选考项目随机选择两项进行训练,试用列举法求小明选择”跳绳![]() 篮球运球“的概率
篮球运球“的概率![]() 提示:可以用字母表示各个项目
提示:可以用字母表示各个项目![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )

A. 7![]() B. 8 C. 7 D. 7
B. 8 C. 7 D. 7![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com