
【题目】某校在学习贯彻十九大精神“我学习,我践行”的活动中,计划组织全校1300名师生到林业部门规划的林区植树,经研究,决定租用当地出租车公司提供的![]() 两种型号的客车共50辆作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量与租车信息:
两种型号的客车共50辆作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量与租车信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 300元/辆 |
| 20人/辆 | 240元/辆 |
注:载客量指的是每辆车客车最多可载该校师生的人数
(1)设租用![]() 型号客车
型号客车![]() 辆,租车总费用
辆,租车总费用![]() 元,求
元,求![]() 与
与![]() 的函数解析式,并直接写出
的函数解析式,并直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过13980元,一共有几种租车方案?哪种租车方案最省钱?
【答案】(1)![]() ,
, ![]() 且
且![]() 为整数.(2)一共有4种租车方案,当租用
为整数.(2)一共有4种租车方案,当租用![]() 型号30辆,
型号30辆,![]() 型号20辆时最省钱.
型号20辆时最省钱.
【解析】
(1)根据租车总费用=每辆A型号客车的租金单价×租车辆数+每辆B型号客车的租金单价×租车辆数,即可得出y与x之间的函数解析式,再由全校共1300名师生需要坐车可求出x的取值范围;
(2)由租车总费用不超过13980元,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其中的整数即可找出各租车方程,再利用一次函数的性质即可找出最省钱的租车方案.
(1)根据题意得:y=300x+240(50-x)=60x+12000,
∵30x+20(50-x)≥1300,
∴x≥30,
∴y与x的函数解析式为y=60x+12000(x≥30);
(2)根据题意得:60x+12000≤13980,
解得:x≤33,
∴共有4种租车方案,方案1:租A型号客车30辆,B型号客车20辆;方案2:租A型号客车31辆,B型号客车19辆;方案3:租A型号客车32辆,B型号客车18辆;方案4:租A型号客车33辆,B型号客车17辆,
∵60>0,
∴y值随x的增大而增大,
∴当x=30时,y取得最小值,
∴租车方案1,即租A型号客车30辆,B型号客车20辆时最省钱.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF. 
(1)求证:DF是⊙O的切线;
(2)若DB平分∠ADC,AB=a,AD:DE=4:1,写出求DE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
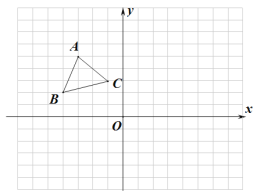
【题目】如图在平面直角坐标系中,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
(1)请你在所给的平面直角坐标系中,画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)将(1)中得到的![]() 向下移动4个单位得到
向下移动4个单位得到![]() ,画出
,画出![]() ;
;
(3)在![]() 中有一点
中有一点![]() ,直接写出经过以上两次图形变换后
,直接写出经过以上两次图形变换后![]() 中对应点
中对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直于x轴、垂足为点B,反比例函数y= ![]() (x<0)的图象经过AO的中点C、且与AB相交于点D,OB=8、AD=6.
(x<0)的图象经过AO的中点C、且与AB相交于点D,OB=8、AD=6. 
(1)求反比例函数y= ![]() 的解析.
的解析.
(2)求经过C,D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )
A.红红不是胜就是输,所以红红胜的概率为 ![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为 ![]()
D.娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com