
(11·贵港)(本题满分12分).
如图,已知直线y=- x+2与抛物线y=a (x+2) 2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
x+2与抛物线y=a (x+2) 2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
(1)请直接写出点A的坐标及该抛物线的解析式;
(2)若P为线段AB上一个动点(A、B两端点除外),连接PM,设线段PM的长为l,点P的横坐标为x,请求出l2与x之间的函数关系,并直接写出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在点P,使以A、M、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)A的坐标是(0,2)………………1分
抛物线的解析式是y= (x+1) 2………………3分
(x+1) 2………………3分
(2)如图,P为线段AB上任意一点,连接PM,过点P作PD⊥x轴于点D…………4分
设P的坐标是(x,- x+2),则在Rt△PDM中,
x+2),则在Rt△PDM中,
PM2=DM2+PD2
即l2=(-2-x)2+(- x+2)2=
x+2)2=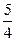 x2+2x+8………………6分
x2+2x+8………………6分
自变量x的取值范围是:-5<x<0………………7分
(3)存在满足条件的点P………………8分
连接AM,由题意得,AM= =
=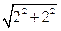 =2
=2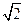 ………………9分
………………9分
①当PM=PA时,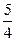 x2+2x+8=x2+(-
x2+2x+8=x2+(- x+2-2)2
x+2-2)2
解得:x=-4 此时 y=- ×(-4)+2=4
×(-4)+2=4
∴点P1(-4,4) ………………10分
②当PM=AM时,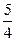 x2+2x+8=(2
x2+2x+8=(2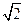 )2
)2
解得:x1=-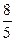 x2=0(舍去) 此时 y=-
x2=0(舍去) 此时 y=- ×(-
×(-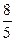 )+2=
)+2=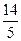
∴点P2(-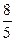 ,
,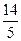 ) ………………11分
) ………………11分
③当PA=AM时,x2+(- x+2-
x+2- 2)2=(2
2)2=(2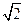 )2
)2
解得:x1=-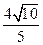 x2=
x2=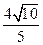 (舍去)
(舍去)
此时 y=- ×(-
×(-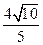 )+2=
)+2=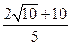
∴点P3(-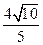 ,
,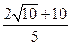 ) ………………12分
) ………………12分
综上所述,满足条件的点为P1(-4,4)、P2(-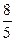 ,
,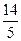 )、P3(-
)、P3(-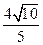 ,
,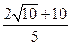 )
)
解析


科目:初中数学 来源: 题型:
(11·贵港)(本题满分11分)
如图所示,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
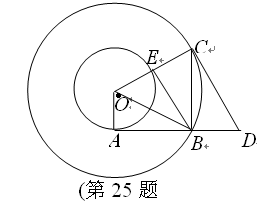
(1)求证:△AOB∽△BDC;
(2)设大圆的半径为x,CD的长为y:
① 求y与x之间的函数关系式;
② 当BE与小圆相切时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·贵港)(本题满分10分)
随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭.据某市交通部门统计,2008年底该市汽车拥有量为75万辆,而截止到2010年底,该市的汽车拥有量已达108万辆.
(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;
(2)为了保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2012
年底全市汽车拥有量不超过125.48万辆;另据统计,从2011年初起,该市此后每年报废的
汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同,请你估算出该市从2011
年初起每年新增汽车数量最多不超过多少万辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·贵港)(本题满分9分)
如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°,CE=2BE,试判断△CDE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
(11·贵港)(本题满分9分)
“校园手机”现象越来越受到社会的关注.为了了解学生和家长对中学生带手机的态度,某记者随机调查了城区若干名学生和家长的看法,调查结果分为:赞成、无所谓、反对,并将调查结果绘制成如下不完整的统计表和统计图:

根据以上图表信息,解答下列问题:
(1)统计表中的A=_ ▲ ;
(2)统计图中表示家长“赞成”的圆心角的度数为_ ▲ 度;
(3)从这次接受调查的学生中,随机抽查一个,恰好是持“反对”态度的学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·贵港)(本题满分6分)
按要求用尺规作图(只保留作图痕迹,不必写出作法)
(1)在图(1)中作出∠ABC的平分线;(2)在图(2)中作出△DEF的外接圆O.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com