Question

19．对于两个已知图形G₁，G₂，在G₁上任取一点P，在G₂上任取一点Q，当线段PQ的长度最小时，我们称这个最小长度为G₁，G₂的“密距”，用字母d表示；当线段PQ的长度最大时，我们称这个最大的长度为图形G₁，G₂的“疏距”，用字母f表示．例如，当M（1，2），N（2，2）时，点O与线段MN的“密距”为$\sqrt{5}$，点O与线段MN的“疏距”为2$\sqrt{2}$．
（1）已知，在平面直角坐标系xOy中，A（-2，0），B（0，4），C（2，0），D（0，1），
①点O与线段AB的“密距”为$\frac{4\sqrt{5}}{5}$，“疏距”为4；
②线段AB与△COD的“密距”为$\frac{3\sqrt{5}}{5}$，“疏距”为2$\sqrt{5}$；
（2）直线y=2x+b与x轴，y轴分别交于点E，F，以C（0，-1）为圆心，1为半径作圆，当⊙C与线段EF的“密距”0＜d＜1时，求⊙C与线段EF的“疏距”f的取值范围．

Answer 1

分析 （1）根据垂线段最短，利用三角形的面积公式即可求得密距，求得线段的端点到O的距离即可求得疏距；
（2）分成当点F在y轴的正半轴时，当点F在y轴的负半轴，两种情况进行讨论，解法与（1）相同．

解答 解：（1）①如图1所示：过点O作OE⊥AB，垂足为E，DF⊥AB，垂足为F．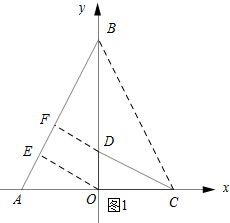

∵A（-2，0），B（0，4），
∴OA=2，OB=4．
∴点O与线段AB的疏距=OB=4．
在Rt△AOB中，由勾股定理得：AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{5}$．
∵S_△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OE，
∴OE=$\frac{AB•OB}{AB}$=$\frac{2×4}{2\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$．
∵FD⊥AB，OE⊥AB，
∴DF∥OE．
∴△BFD∽△BEO．
∴$\frac{DF}{OE}=\frac{BD}{OB}$，即DF=$\frac{3}{4}$OE=$\frac{3}{4}×\frac{4\sqrt{5}}{5}$=$\frac{3\sqrt{5}}{5}$．
∴△ODC与线段AB的密距为=$\frac{3\sqrt{5}}{5}$．
在△OBC中，BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$．
∴△ODC与AB的数据为2$\sqrt{5}$．
故答案为：①$\frac{4\sqrt{5}}{5}$；4；②$\frac{3\sqrt{5}}{5}$；2$\sqrt{5}$．
（2）①当点F在y轴的正半轴时，如图2．
当E在O时，密距时0，此时疏距是2．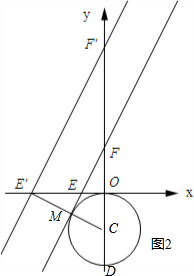

CE'=2，OC=1，
则OE'=$\sqrt{CE{'}^{2}-O{C}^{2}}$=$\sqrt{3}$．
在直角△OE'F'中，OF'=2OE'=2$\sqrt{3}$，
则此时，疏距是2$\sqrt{3}$+2．
所以2＜f＜2$\sqrt{3}$+2．
②当点F在y轴的负半轴时，如图3所示．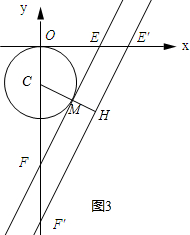

∵EF的解析式为y=2x+b，
∴tan∠OEF=2，
∴OE：EF=1：$\sqrt{5}$．
当d=0时，MC=1，直线EF与圆C相切，则∠CMF=∠EOF=90°，
又∵∠OFE=∠CFM，
∴△CMF∽△EOF．
∴$\frac{CM}{CF}=\frac{OE}{EF}$，即$\frac{1}{CF}=\frac{1}{\sqrt{5}}$
当d=1时，
如图3，QH=1，则PH=2，
∵Rt△PHF∽Rt△OEF，
∴PF=2$\sqrt{5}$，
∴OF=2$\sqrt{5}$+1，
∴$\sqrt{5}$+1＜f＜2$\sqrt{5}$+1．
当点F在y轴的负半轴时，
当d=0时，如图2，f=$\sqrt{5}$+1；
当d=1时，
如图3，QH=1，则PH=2，
∵Rt△PHF∽Rt△OEF，
∴PF=2$\sqrt{5}$，
∴OF=2$\sqrt{5}$+1，
∴$\sqrt{5}$+1＜f＜2$\sqrt{5}$+1．
综上所述，当0＜d＜1时，f的取值范围，$\sqrt{5}$+1＜f＜2$\sqrt{5}$+1．

点评 本题考查了一次函数的应用和相似三角形的判定与性质，正确理解题目中介绍的“密距”和“疏距”的定义是关键．