
【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发xmin后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).

(1)A点所表示的实际意义是 ;![]() = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度
的一半,那么两人出发后多长时间第一次相遇?
【答案】![]() ;y=-360x+1200;x=2.5
;y=-360x+1200;x=2.5
【解析】
(1)根据已知M点的坐标进而得出上坡速度,再利用已知下坡的平均速度则是各自上坡平均速度的1.5倍,得出下坡速度以及下坡所用时间,进而得出A点实际意义和OM,AM的长度,即可得出答案;
(2)根据A,B两点坐标进而利用待定系数法求出一次函数解析式即可;
(3)根据小刚上坡平均速度是小亮上坡平均速度的一半首先求出小刚的上坡的平均速度,进而利用第一次相遇两人中小刚在上坡,小亮在下坡,即可得出小亮返回时两人速度之和为:120+360=480(m/min),进而求出所用时间即可.
(1)根据M点的坐标为(2,0),则小亮上坡速度为:![]() =240(m/min),则下坡速度为:240×1.5=360(m/min),
=240(m/min),则下坡速度为:240×1.5=360(m/min),
故下坡所用时间为:![]() (分钟),
(分钟),
故A点横坐标为:2+![]() =
=![]() ,纵坐标为0,得出实际意义:小亮出发
,纵坐标为0,得出实际意义:小亮出发![]() 分钟回到了出发点;
分钟回到了出发点;
 .
.
故答案为:小亮出发![]() 分钟回到了出发点;
分钟回到了出发点;![]() .
.
(2)由(1)可得A点坐标为(![]() ,0),
,0),
设y=kx+b,将B(2,480)与A(![]() ,0)代入,得:
,0)代入,得: 
解得![]() .
.
所以y=360x+1200.
(3)小刚上坡的平均速度为240×0.5=120(m/min),
小亮的下坡平均速度为240×1.5=360(m/min),
由图象得小亮到坡顶时间为2分钟,此时小刚还有4802×120=240m没有跑完,两人第一次相遇时间为2+240÷(120+360)=2.5(min).


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
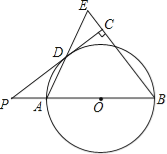
(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 边长为
边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() ,
,![]() 上当
上当![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在边
随之在边![]() 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,制定了促销条件:当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元.
(1)若销售商一次订购x(x>100)个零件,直接写出零件的实际出厂单价y(元)?
(2)设销售商一次订购x(x>100)个零件时,工厂获得的利润为W元(W>0).
①求出W(元)与x(个)之间的函数关系式及自变量x的取值范围;并算出销售商一次订购多少个零件时,厂家可获得利润6000元;
②厂家为了达到既鼓励销售商订购又保证自己能获取最大利润的目的,重新制定新促销条件:在原有的基础上又增加了限制条件﹣﹣销售商订购的全部零件的实际出厂单价不能低于a(元).请你利用函数及其图象的性质求出a的值;并写出实行新促销条件时W(元)与x(个)之间的函数关系式及自变量x的取值范围.(工厂出售一个零件利润=实际出厂单价﹣每个零件的成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P,Q分别是等边△ABC边AB,BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ,CP交于点M.
(1)求证:△ABQ![]() △CAP;
△CAP;
(2)如图1,当点P,Q分别在AB,BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P,Q在分别运动到点B和点C后,继续在射线AB,BC上运动,直线AQ,CP交点为M,则∠QMC= 度.(直接填写度数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,动点
,动点![]() 从点
从点![]() 开始沿
开始沿![]() 以每秒
以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,动点
移动,动点![]() 从点
从点![]() 开始沿
开始沿![]() 以每秒
以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动.如果
移动.如果![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间
(秒)表示移动的时间![]() ,那么:
,那么:
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 是梯形,此时梯形
是梯形,此时梯形![]() 的面积是多少?
的面积是多少?
![]() 当
当![]() 为何值时,以点
为何值时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
![]() 若设四边形
若设四边形![]() 的面积为
的面积为![]() ,试写出
,试写出![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 取何值时,四边形
取何值时,四边形![]() 的面积最小?
的面积最小?
![]() 在
在![]() 轴上是否存在点
轴上是否存在点![]() ,使点
,使点![]() 、
、![]() 在移动过程中,以
在移动过程中,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形的面积是一个常数?若存在请求出点
为顶点的四边形的面积是一个常数?若存在请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用所学函数知识,对函数![]() 进行了如下研究.列表如下:
进行了如下研究.列表如下:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |

(1)自变量x的取值范围是________;
(2)表格中:m=_______;n=________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______________.
的图象交点的坐标为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com