

分析 连A1A5,A1A4,A1A3,作A6C⊥A1A5,利用正六边形的性质分别计算出A1A4=2a,A1A5=A1A3=3$\sqrt{3}$,而当A1第一次滚动到图2位置时,顶点A1所经过的路径分别是以A6,A5,A4,A3,A2为圆心,以3,3$\sqrt{3}$,6,3$\sqrt{3}$,3为半径,圆心角都为60°的五条弧,然后根据弧长公式进行计算即可.
解答 解:连A1A5,A1A4,A1A3,作A6C⊥A1A5,如图,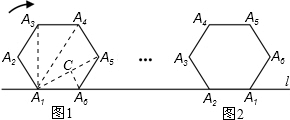
∵六边形A1A2A3A4A5A6为正六边形,
∴A1A4=6,∠A1A6A5=120°,
∴∠CA1A6=30°,
∴A6C=$\frac{3}{2}$,A1C=$\frac{3\sqrt{3}}{2}$,
∴A1A5=A1A3=3$\sqrt{3}$,
当A1第一次滚动到图2位置时,顶点A1所经过的路径分别是以A6,A5,A4,A3,A2为圆心,
以3,3$\sqrt{3}$,6,3$\sqrt{3}$,3为半径,圆心角都为60°的五条弧,
∴顶点A1所经过的路径的长=$\frac{60π×3}{180}$+$\frac{60π×3\sqrt{3}}{180}$+$\frac{60π×6}{180}$+$\frac{60π×3\sqrt{3}}{180}$+$\frac{60π×3}{180}$=(4+2$\sqrt{3}$)π,
故答案为:(4+2$\sqrt{3}$)π.
点评 本题考查了轨迹,弧长公式:l=$\frac{nπr}{180}$,也考查了正六边形的性质以及旋转的性质,难度一般.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 3 | 2 | 1 | 0 | -1 | -2 |
| A. | x<1 | B. | x>1 | C. | x<0 | D. | x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com